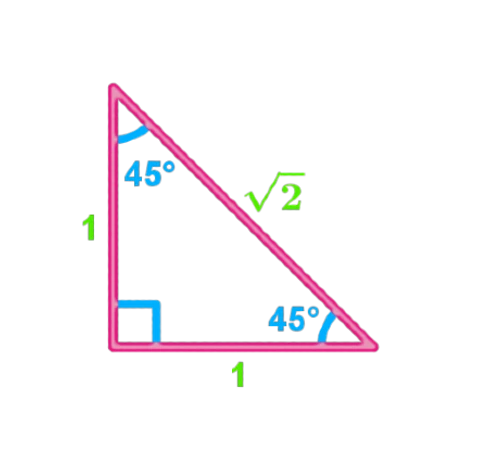
45 45 90 Triangle Ratio, Formula & Sides

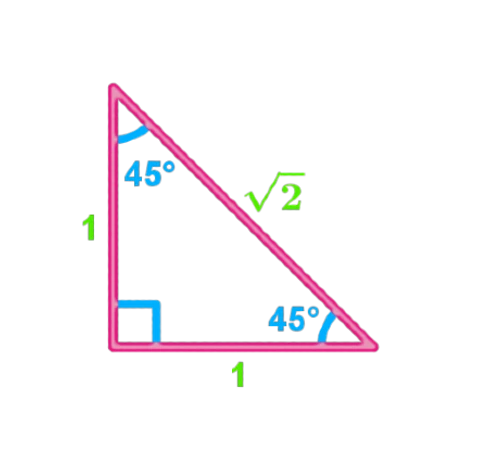
What is 45 45 90 Triangle (Isosceles Right Triangle)?

The 45-45-90 triangle gets its name from two equal angles and a right angle. The sides corresponding to both equal angles are of equal length. Therefore, this triangle is an isosceles triangle since both sides of the triangle are the same length. An angle of 90 degrees is called a right angle. Therefore, this triangle is defined as an isosceles right triangle. The 45 45 90 triangle is an important type of triangle, especially used in practical calculation and geometry problems.

Rule

The length of the hypotenuse is √2 times the length of the other two sides. So, in a 45 45 90 triangle with two sides of length x, the length of the hypotenuse is x√2.

Properties

According to these angles, some properties of the special triangle are as follows:

• This particular right triangle is also an isosceles triangle. An isosceles triangle is a triangle with two sides of equal length. Both angles are equal.
• The length of the hypotenuse is √2 times the length of the other two sides. So, in a 45 45 90 triangle with two sides of length x, the length of the hypotenuse is x√2.
• The lengths of both perpendicular sides are equal.
• It is used in various ways along with other types of triangles. For example, half of the square is a 45 45 90 triangle, which can be used to bisect or scale the square.

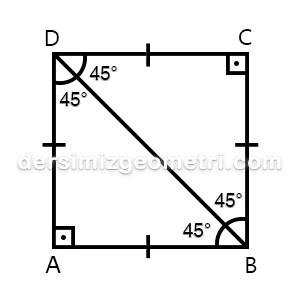
• The sum of the interior angles of a triangle is 180 degrees. The 45 45 90 triangle has two equal 45 degree angles because one angle is right.
• Since the 45 45 90 triangle is a type of triangle in which both sides are equal, this property is sometimes used in practical calculations and scaling operations.
• Because of these properties, the 45 45 90 triangle is used in mathematics, engineering, physics, architecture and many other fields. It is particularly useful for practical computing and scaling operations.