Geometry Formulas

What does a geometry formulas mean? How to facilitate learning all important geometry formulas? How to memorize triangle and quadrilateral formulas, and how not to forget them? What is the importance of keeping the common geometry formulas in mind? If you want to find out, take a look at this article.
Geometry is a branch of mathematics. It is related to distance, shape, size, and figures. By being aware of geometry all formulas, being successful in this field is achievable. This article is written to show you the geometry practical formulas. Because knowing the geometric formulas makes it easier for you to solve geometry problems. To memorize the geometry formulas and not to forget them, you can take a look at this article.
Angles in Geometry
As mentioned before, geometry is a branch that is related to many different aspects of figures. And one of them is angles. Analytical geometry formulas help people to understand more about appearances. Therefore, being aware of their importance, and memorizing them are necessities. Calculating an angle depends on various factors like the calculation of the area. Formulas related to the angles are among the common geometry formulas. By being aware of the angles in geometry, you can increase your success in this field.
Angles of Triangles
Every shape must have an angle. Therefore, triangles also have angles. There are two types of angles of triangles, which are interior and exterior. The interior angles represent the three angles found inside a triangle. On the other hand, the exterior ones describe the angles which are extended to infinity. To find out more about angles triangles geometry formulas, taking a look at the pictures below is a must.
Angles of Quadrilaterals
Geometry formulas angles vary. Therefore, it’s a broad subject that covers many formulas. The types of angles, which are interior and exterior, apply for quadrilaterals as well. The only difference is their value. While interior angles of a triangle add up to 180 degrees, this number is 360 degrees for quadrilaterals. Knowing the angles of quadrilaterals is essential for solving the questions related to the geometry formulas.
Area in Geometry
Geometry area formulas take an important spot among all of the formulas. Since this is a branch that is related to figures, becoming conscious of how to calculate each figure’s area is essential for success. You can learn more about geometry area formulas by taking a look at the pictures. It is for sure that no academic success is achievable unless you understand the area in geometry comprehensively.
The Triangle’s Area
There are different types of triangles. Therefore, calculating the triangle’s area varies based on their types. Learning how to calculate the area of a triangle is possible by memorizing the geometry formulas triangles. The four kinds of triangles are equilateral, isosceles, right-angled, and scalene. You can learn their formulas through the pictures below.
The Quadrilateral’s Area
There are also quadrilateral formulas for the calculation of area. Just like triangles, since there are numerous kinds of quadrilaterals, there is no single formula. The types of quadrilateral are rectangle, square, parallelogram, trapezium or trapezoid, and rhombus. You can find the quadrilateral’s area formulas by examining the pictures. While there are a number of formulas, it is easy to memorize these two-dimensional, four-sided figures’ areas.
Analytical Geometry
Analytical geometry is a subcategory of this branch that is related to the coordinate system. Therefore, it is also called coordinate geometry. There are numerous analytical geometry formulas that would help you to understand this subject. There are various topics of this, such as linear algebra, vector space, ellipse, calculus. These topics show the importance of memorizing general formulas, such as circle analytics formulas.
Analytics of the Circle
Since the analysis of the circle is for establishing a base between geometric curves and algebraic equations, you need to be conscious of the formulas. When the topic is about the circle in analytical geometry, there are two important terms, which are radius and center. To perform the circle analytics formulas, these terms hold important spots.
Radius and Center
Radius defines the equality in the distance of all points of a circle from the given point. The given point is the center. So, if the question doesn’t involve a picture, you need to sketch your own circle and decide on the equation of the circle. And finally, you should calculate the length. In this way, radius and center can be seen obviously. Since this topic is essential among the geometry formulas, you should practice as much as you can.
A Geometric Sequence
A geometric sequence of a geometric progression is a sequence of numbers other than zero. There are different kinds of progressions. That’s why the geometric series sum formula depends on the type of the sequence. The three major types of sequence are arithmetic, geometric, and Fibonacci sequences. To find out more about the geometric series sum formula, you can take a look at the pictures of formulas and scan the definitions of sequences below. While you are taking a skim of the formulas, you need to know that (1) a is the first term, (2) r is the common ratio, and (3) n is the number of the terms that should be measured.
Arithmetic Sequence
An arithmetic sequence is a progression that contains successive terms. Throughout the sequence, the same common difference can be seen. Since it is linear, it is easy to calculate a number by simple formulas, such as the geometry mean formula.
Geometric Sequence
Another type of sequence is the geometric sequence. It does not have a common difference. Instead, it has the same common ratio. Thus, it is a non-linear progression. However, it is still easy to calculate the terms of it.
Fibonacci Sequence
The final type is a Fibonacci sequence. It is an unusual and more rare type than others. That’s why it is not included in the general geometry formulas. Because it does not represent a visible pattern. So, it is hard to perform the geometric series sum formula in this case. Another name for this progression is the recursive formula.
Sum of the Sequences
he Sum of the sequences can be measured based on different formulas. There are different formulas because there are different kinds of sequences. Based on the type, you should measure the result. However, even geometric sequences sum formula for the arithmetic sequence have various types. Therefore, you need to learn the basics. The first step is to determine the kind of sequence. Thereafter, you should identify the numbers, and measure the difference between the numbers. After writing down the first and last numbers of the sequence, you can apply the geometric sequences sum formula successfully.
Transformation Geometry
Another topic of geometry is transformation geometry. Since there are numerous types of transformation, transformation geometry formulas change depending on the type. The major types of transformation are rotation, reflection, translation, resizing, congruent, similar symmetry index, and geometry index. By taking a look at geometry formulas, you can be more conscious about this topic.
Rotation of Figures
Rotation of the figures means turning around a center. Center is the keyword here. To solve the questions correctly, you need to keep them in mind. Rotation is among the important transformation geometry formulas. So, you should practice.
Reflection of Figures
Every figure has a reflection. The reflections should have the same size with the real image. This is the thing you need to be aware of the most while sketching the reflection of figures. Since this topic is among the geometry formulas, you should exercise as much as you need. While sketching, you should draw a central line which is also called a mirror line. Based on the position of the line, the reflection is called horizontal, vertical, or diagonal reflection.
Translation of Figures
While moving or rotating the figures, you need to put some points on them. This rule also applies to the translation of figures. Because the shapes’ points must move in the direction and move in the same distance. In this way, geometry practical formulas can be applied successfully.
The Angle Side Relations
Another topic of the geometry formulas is the angle side relations. Since there is a connection between these phenomenons, it is essential to learn them to have a high score. These relations depend on the figure and the number of sides. Before taking a look at the rules, you can go above to learn more about geometry formulas angles.
Triangles
In triangles, the relations between angles and sides are clear. Angles triangles geometry formulas clarify the connection. And these connections are accurate for every triangle. The side opposite to the largest angle is the largest in the triangle. In addition to that, the side opposite to the smallest angle is the smallest. Finally, the mid-sized side and mid-sized angles are opposite to each other.
Quadrilaterals
Just like the relations between sides and angles in triangles, the association is also valid for quadrilaterals. Since there are different kinds of quadrilaterals, such as rectangle, square, parallelogram, rhombus, and trapezium, the formulas vary. Therefore, when you think of quadrilateral formulas, you need to think of the shape first.
Conclusion
As you realize throughout the article, there are numerous formulas you should be familiarized with. By being aware of the geometry all formulas, you can increase your success in this lesson. Geometry is a branch of mathematics that is about figures, and their sizes, distances, and shapes. It is essential for you to understand the basics of the subjects before memorizing geometry formulas sheet. In this way, the formulas become more permanent. And you wouldn’t struggle during memorization or keeping in mind.
Some of the main topics of geometry are area, angles, analytics, sequence, transformation, and the relationship between side and angle. Among these topics, geometry triangle formulas, and angle side relations formulas have important spots. By studying the formulas one by one, memorizing them solidly, and exercising on a regular basis, it is possible for every student to have a high score in the university extrance exam. Geometry is an easy field as long as you practice.
You can review the images and download the list of all geometry Formulas PDF format from the end of the page to your computer.
Angles in a concave quadrilateral formula

In a concave quadrilateral as in the figure, (the measure of the angle formed when the triangle’s edge is bent in) it is formulated with x = a + b + c.
Angle of a triangle formula

The angle formed by two inner bisectors in a triangle is 90 ° more than half the size of the inner angle in the third corner.
The angle between the external bisectors of two angles of a triangle

The measure of the angle formed by the two outer bisectors in a triangle is all half the measure of the angle in the third corner. In other words, the angle formed by the two outer bisectors in a triangle is less than 90 ° by half the angle in the third corner.
Internaland the external bisector angle formula

The angle between internal bisector of one base angle and the external bisector of the other base angle of a triangle is equal to one half of the vertical angle.
Triangle inequality theorem

The sum of the lenghts of any two sides of a triangle is greater than the lenght of the third side.
If the side lengths of triangle ABC in the figure are a, b, c; |b-c|<a<b+c, |a-c|<b<a+c, |a-b|<c<a+b.
Perimeter formula of a triangle

The sum of the lengths of any point taken in a triangle ABC to the vertices of the triangle; half of the triangle is larger than its circumference and smaller than its circumference.
In the triangle ABC in the figure, where | BC | = a, | AC | = b, | AB | = c and a + b + c = 2u; u <| KA | + | KB | + | KC <2u.
Thales theorem formula

Thales’s Theorem or Basic Proportionality Theorem states that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
In the figure d1 // d2 // d3, if m and n lines intersect; | AB | / | BC | = | DE | / | EF |, | AB | / | AC | = | DE | / | DF | and | BC | / | AC | = | EF | / | DF |.
Median of a right triangle formula

In the case of a right triangle, the median to the hypotenuse has the property that its length is equal to half the length of the hypotenuse. In other words, in a right triangle the midpoint of the hypotenuse is equidistant from the vertices.
In triangle ABC in the figure, m (A) = 90 ° and | BD | = | DC | if; | BD | = | DC | = | AD |.
Special right triangles properties

30 60 90 triangle rule
Formula (9): The side opposite to 30° angle in a right-angled triangle is half of the hypotenuse. If the length of the hypotenuse is given, divide it by 2 for the shorter leg. Then multiply that result by
√3 to get the length of the longer leg.
15 75 90 triangle rule
Formula (10): In a 15 ° 75 ° 90 ° right triangle, the height of the hypotenuse is one quarter of the hypotenuse.
Isosceles triangle rule-1

In an isosceles triangle, the sum of the posts lowered to equal sides from a point taken on the base is equal to a height belonging to the equal sides.
In the figure; If | AB | = | AC |, [DF] ⊥ [AC], [DE] ⊥ [AB]; | BN | = | ED | + | DF |.
Isosceles triangle rule-2

In an isosceles triangle, the sum of the lengths of the parallel line segments drawn from a point on the base to equal sides is equal to the length of one of the equilateral sides.
Isosceles triangle rule-3

The absolute value of the difference in lengths of the perpendiculars descending to the equal sides of the triangle from a point taken on the extension of the base of the isosceles triangle is equal to a height belonging to the equal sides.
In the figure; If | AB | = | AC |, [EP] ⊥ [AC], [EF] ⊥ [AF] and [BN] ⊥ [AC]; | EP | – | EF | = | BN |.
Isosceles triangle rule-4

The square of the length of the line segment drawn from the vertex to the base in an isosceles triangle is equal to the difference of the length of the sides divided by the square of the length of one of the equilateral sides.
In the triangle ABC in the figure, with | AB | = | AC | = b, | AD | = x, | BD | = m and | DC | = n; x² = b²-m.n.
Equilateral triangle rule

In the figure, if ABC is an equilateral triangle, [DE] ⊥ [AE], [DT] ⊥ [BC], [DF] ⊥ [AF] | AB | √3 / 2 = | ED | + | DF | – | DT |.
Angle bisector theorem

An angle of a triangle divides the interior angle’s opposite side into two segments that are proportional to the other two sides of the triangle.
If the triangle ABC in the figure [AN] is the bisector; | AB | / | BN | = | AC | / | CN |.
External bisector theorem

External bisector of an angle of a triangle divides opposite side in ratio of sides containing angle.
In triangle ABC in the figure [AD]; the bisector of m (CAE), with | CD | = x, | BC | = a, | AC | = b and | AB | = c; x / (x + a) = b / c
Internal and external bisector formula
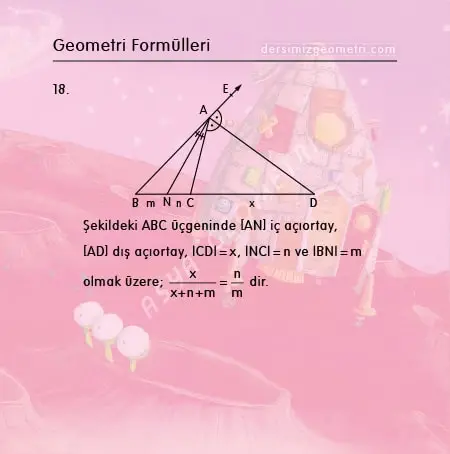
In the triangle ABC in the figure, [AN] internal bisector, [AD] external bisector, | CD | = x, | NC | = n and | BN | = m; x / (x + n + m) = n / m.
External bisector rule

In the triangle ABC in the figure, [AD] external bisector, | CD | = x, | BC | = a, | AC | = b, | AB | = c and | AD | = y; y² = x. (x + a) -bc.
Right triangle side length rule

In a right triangle, the hypotenuse is found by multiplying the lengths of the sides and dividing by the length of the hypotenuse.
In the triangle ABC in the figure, [BA] ⊥ [AC], [AD] ⊥ [BC], | AB | = c br, | AC | = b br, | BC | = a br and | AD | = h br ; right triangle side length rule is h = (c.b) / a is the unit.
The median of a triangle divides it into two triangles of equal areas

The median of a triangle divides it into two triangles of equal areas.
In the triangle ABC in the figure, | BF | = | FC | if; Area (ABF) = Area (AFC).
Angle bisectors of a triangle

Every triangle has one point that is equidistant from all three sides of the triangle. This is the point in which the angle bisectors of all the angles of the triangle intersect. Using this point as the centre we can draw a circle that touches all three sides of the triangle. This is called the inscribed circle of the triangle.
If [BP], [CP] in triangle ABC in the figure; [AP] is bisector.
Median of a triangle formula
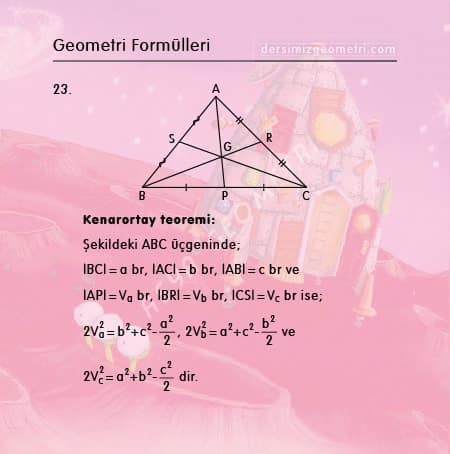
In any median of a triangle, the distance between the center of gravity (or centroid) G and the center of its corresponding side is one third (1/3) of the length of that median, the centroid is two thirds (2/3) of the distance from each vertex to the midpoint of the opposite side.
In the triangle ABC in the figure, if BC | = a br, | AC | = b br, | AB | = c br, | AP | = Va br, | BR | = VB br, | CS | = VC br; median of a triangle formula is 2Va² = b² + c²-a² / 2, 2Vb² = a² + c²-b² / 2 and 2Vc² = a² + b²-c² / 2.
Median length formula

Formula (24): A triangle ABC with side lengths a, b, c and median lengths Va, Vb, Vc; median length formula is 4 (Va² + Vb² + Vc²) = 3 (a² + b² + c²).
Area of a triangle with the inradius
Formula (25): The semiperimeter of the triangle, lets call it u, is (a + b + c)/2 which means that we can write the formula for the area of a triangle as: Area (ABC) = u.r
If the radius r of the inner tangent circle of a triangle, the sides are a, b, c and semiperimeter (u) = (a + b + c) / 2; Area (ABC) = u.r
Area of concave quadrilateral formula

If m (ADB) = α in triangle ABC in the figure; area of the concave quadrilateral (polygon) formula is A (ABEC) = (1/2). | AE |. | BC | .sineα.
Area of quadrilateral formula

Area of a quadrilateral the product of the two diagonals times the sine of their included angle.
In any quadrilateral; diagonals | CA | = e, | DB | = f with angle between α; area of quadrilateral formula = (1/2) .e.f.sineα.
Orthodiagonal quadrilateral formula (a rule)

if the diagonals of a quadrilateral are perpendicular, the sum of squares of opposite sides is equal to each other. (a² + c² = b² + d²). It also doesn’t have to be a rhombus. 🙂
Right trapezoid formula

In a right trapezoid, if the diagonals are perpendicular to each other, the height is the geometrical middle of the lower and upper base. (Height squared equals the product of the bases.)
The quadrilateral ABCD in the figure is [CD] ⊥ [DA], [DA] ⊥ [CD], [DB] ⊥ [AC], | AB | = a br, | CD | = c br and | DA | = h br; h = √ac.
Area of a triangle in a trapezoid (a rule)

The midpoint of one of the side edges in a trapezoid; the area of the triangle obtained when joined by two opposite vertices is equal to half the area of the trapezoid.
ABCD trapezoid and | CA | = | DB | if; Area (DAE) = (1/2) . Area (ABCD).
Formula of the area of parallelogram inscribed in a quadrilateral

If the midpoints of the sides of a quadrilateral are connected, a parallelogram is formed.
The midpoints of the N, P, K, L sides in the quadrant ABCD in the figure; Area (NPKL) = (1/2). Area (ABCD).
Area of a parallelogram (a rule)

The sum of the areas of the two triangles obtained when any point taken outside the parallelogram is joined to the vertices of the parallelogram is equal to half the area of the parallelogram.
In the figure ABCD is a parallelogram and a point P taken outside; Area (PDA) + Area (PBC) = (1/2). Area (ABCD).

Geometry Formulas PDF
Course Geometry offers Geometry textbook in pdf format that can be downloaded free of charge. Students can view the geometry formulas pdf, which is important for university entrance exam, which aims to improve students’ problem solving skills.