Geometry Notes

In Geometry Notes, we have answered the classical and new generation questions that are highly likely to appear in exams. We did this with a clear and simple explanation without causing confusion. More importantly, it is among our aims to enable you to look at the problems from a broad perspective and to interpret them correctly.

Here are some resources for free geometry notes:

MathPlanet: MathPlanet offers free geometry notes covering a wide range of topics, including Euclidean geometry, transformations, and coordinate geometry.

Purplemath: Purplemath offers free geometry notes that cover basic concepts and advanced topics such as proofs, circles, and trigonometry.

Math Open Reference: Math Open Reference is a free online geometry textbook that provides clear explanations and interactive diagrams for a variety of geometry topics.

Math Is Fun: Math Is Fun offers free geometry notes and interactive tutorials that cover a range of topics from basic shapes to coordinate geometry.

Khan Academy: Khan Academy provides free geometry notes and video lessons covering a range of geometry topics, from points and lines to three-dimensional geometry.

These are just a few examples of the many resources available online for free geometry notes. You can also check with your school or university’s math department to see if they offer additional resources or materials.

Even if you’re a student in a classroom, if you don’t take math-geometry grades properly and always write them on the back of the paper, you don’t have the concept of “review” or “topic repetition”, so you won’t have grades. If you don’t understand something in a topic or problem, be it a Mathematics-Geometr Course or any other course, you tend to get bored with writing notes.

If you quit, you won’t even think about going back and reviewing it later. Even if you don’t understand a problem during class, when you get home, you can look at your notebook and say, “It’s really simple!” you might think! Please do your best not to leave your geometry notebook empty.

Geometry Worksheets

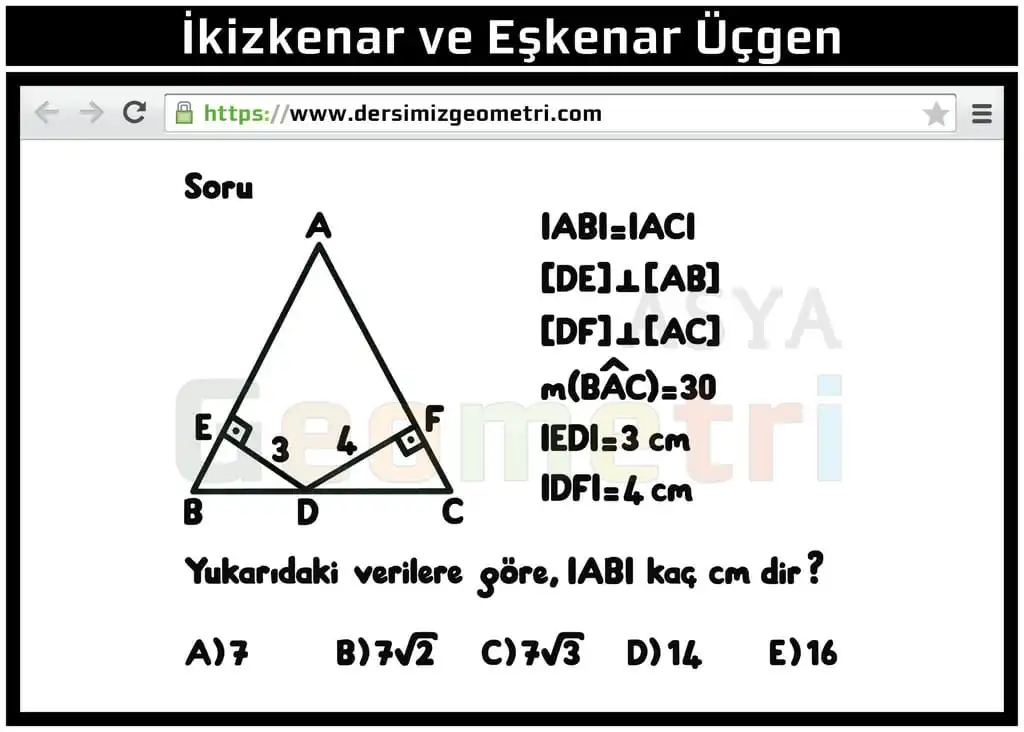
In ABC isosceles triangle (| AB | = | AC |), [DE] perpendicular [AB], [DF] perpendicular [AC], m (BAC) = 30 °, | ED | = 3 cm, | DF | = 4 cm if; | AB | how many cm?

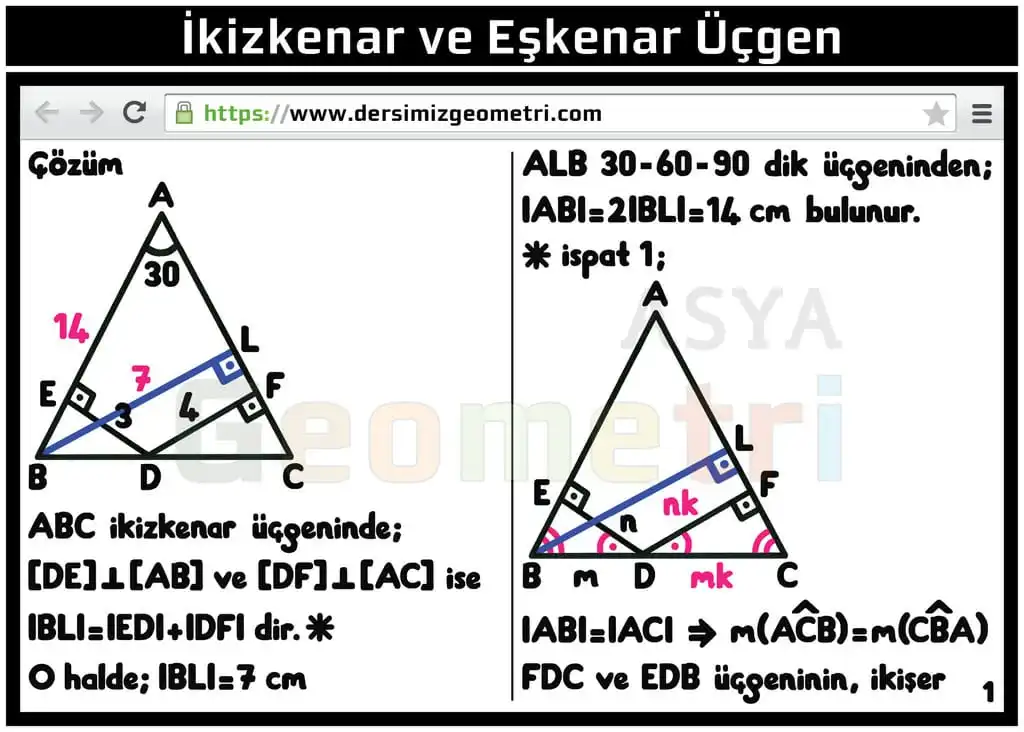
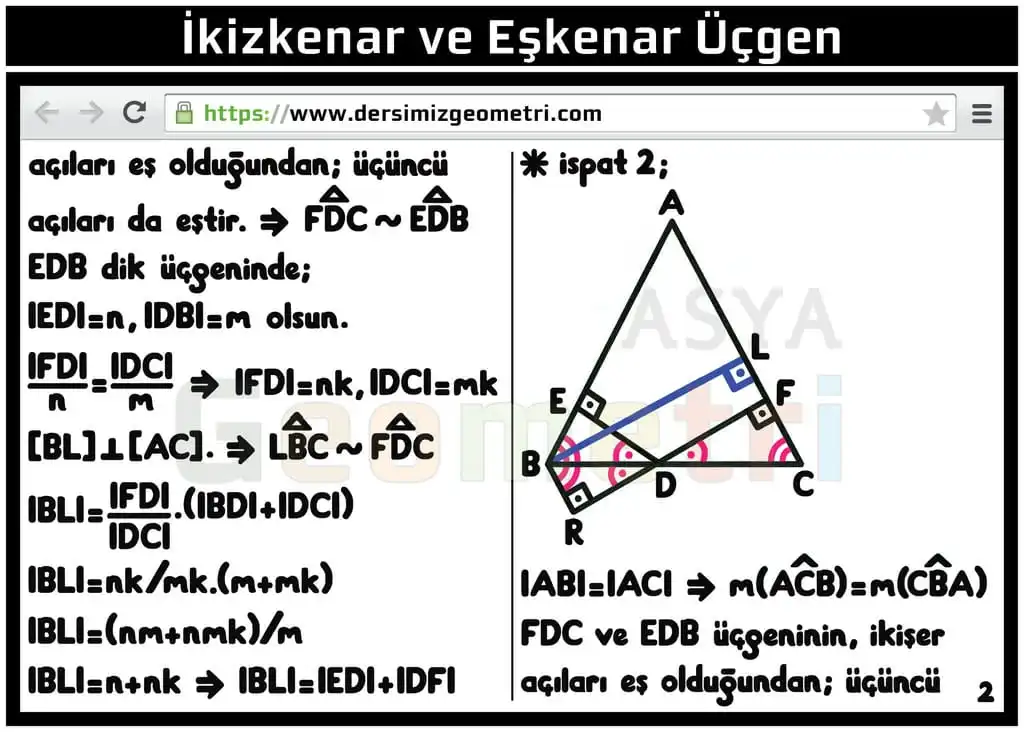
In an isosceles triangle, the sum of the posts lowered to equal sides from a point taken on the base is equal to a height belonging to the equal sides. (An isosceles triangle proof)

ABC equilateral triangle, if m (AFB) = 150 °, | FB | = 8 cm, | FC | = 17 cm; | AF | = how many cm is x?

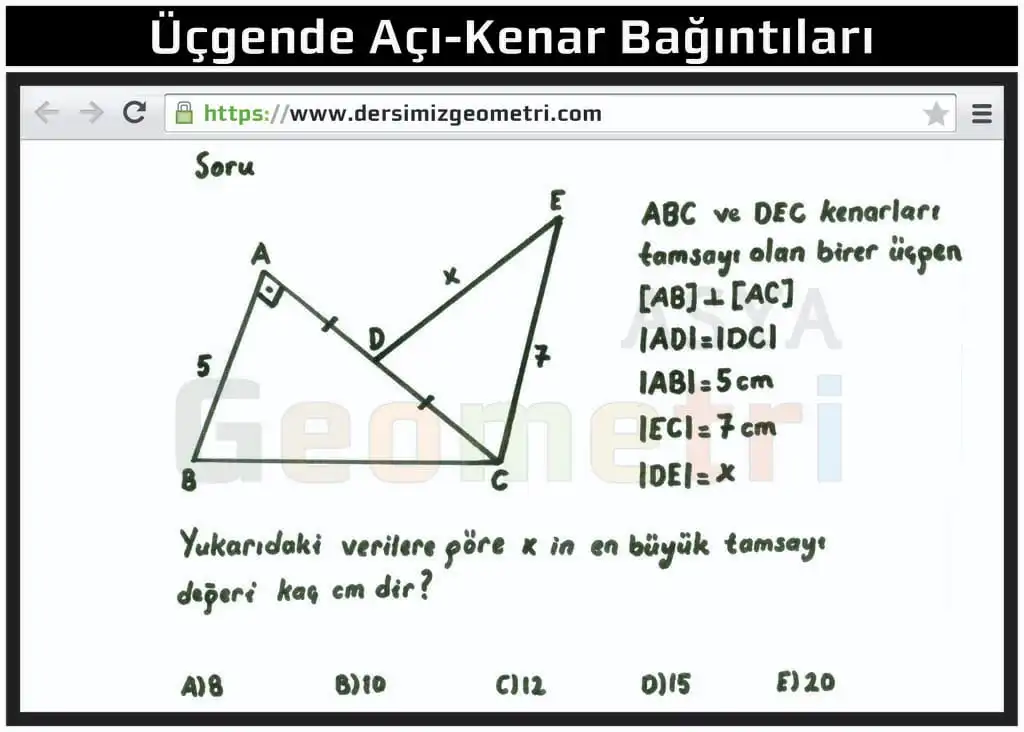
ABC and DEC are triangles with integer sides, [AB] perpendicular [AC], | AD | = | DC |, | AB | = 5 cm, | EC | = 7 cm; How many cm is the largest integer value of | DE | = x?

ABC is a triangle, if m (BAD) = m (DAC) = 60 °, | AB | = 6 cm, | AD | = 4 cm; | DC | = how many cm is x?

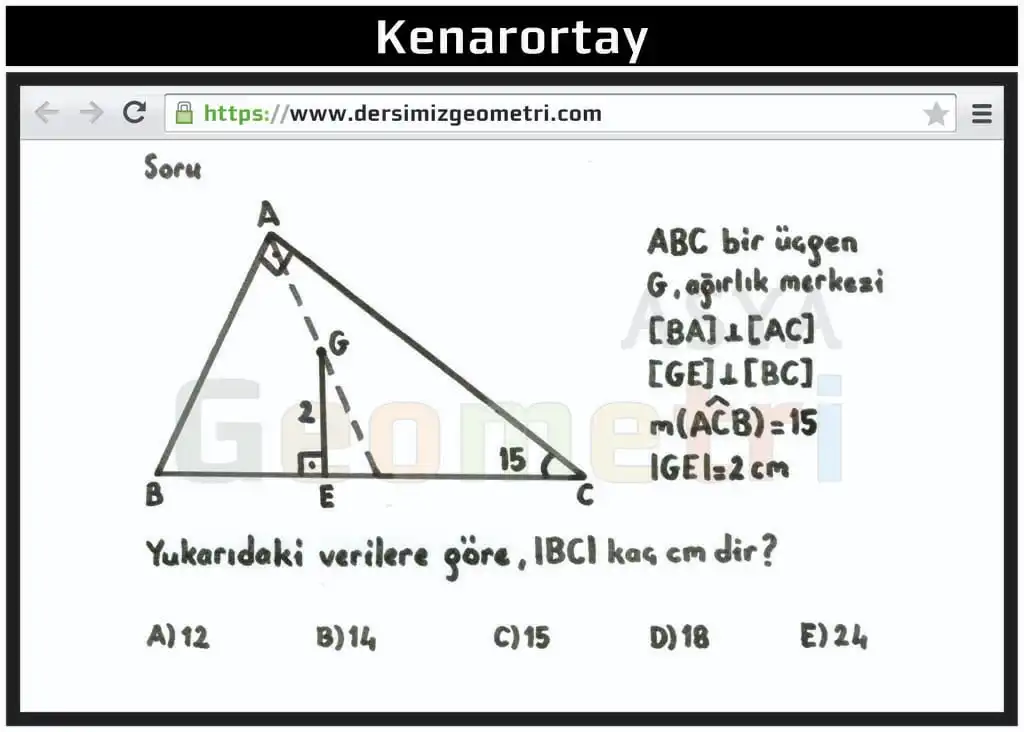
ABC is a triangle, center of gravity G, [BA] perpendicular [AC], [GE] perpendicular [BC], if m (ACB) = 15 °, | GE | = 2 cm; | BC | how many cm?

ABC is an isosceles triangle shaped cardboard, [AH] perpendicular [BC], | AB | = | AC |, | AH | = 25 cm. When folded along [DE], corner A coincides with corner C. [DE] ∩ [AH Since] = {K}; | AK | how many cm?

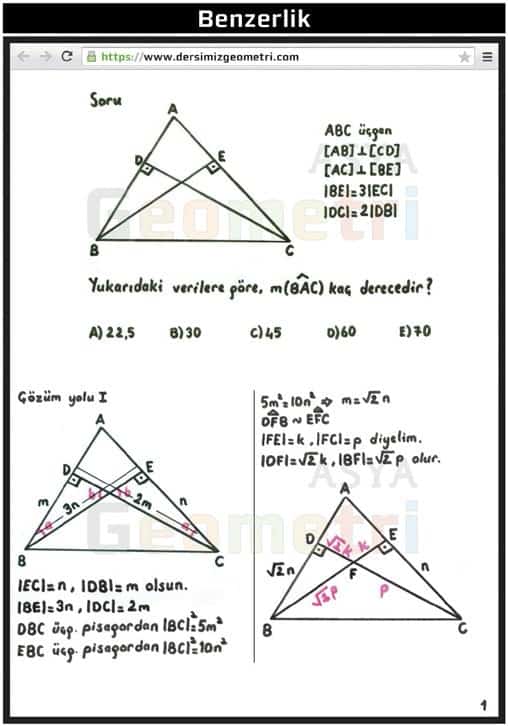
ABC triangle, [AB] perpendicular [CD], [AC] perpendicular [BE], | BE | = 3 | EC |, | DC | = 2 | DB | if; How many degrees is m (BAC)?

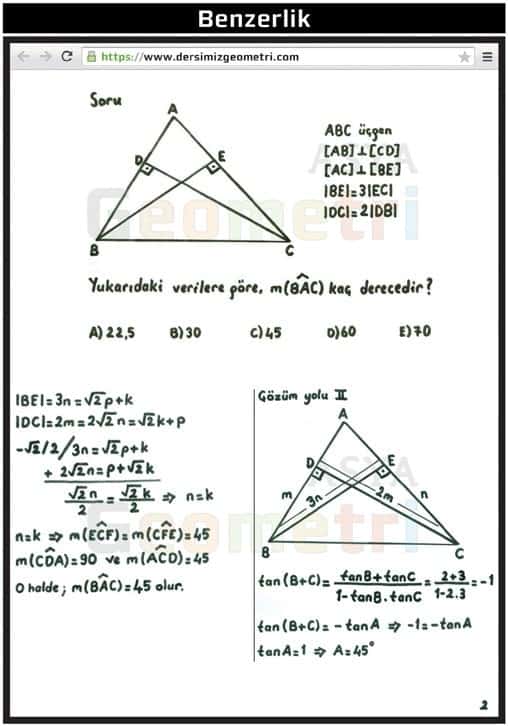
Üçgen sorusunun diğer bir çözümü (Trigonometri ile çözüm)

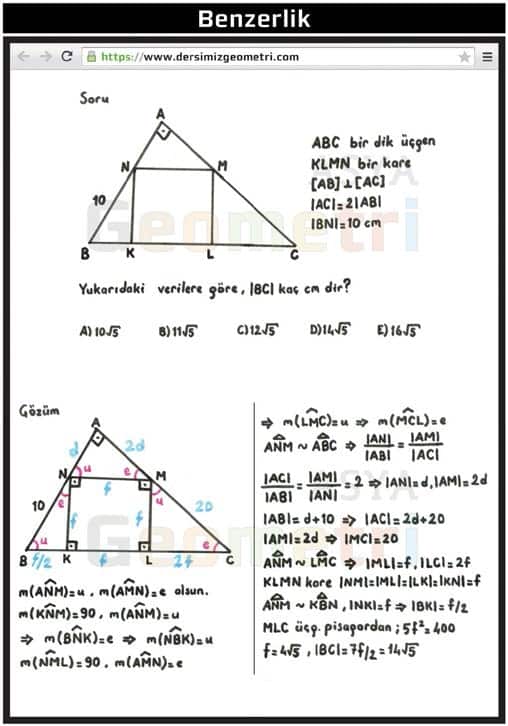
ABC is a right triangle, KLMN is a square, [AB] perpendicular [AC], | AC | = 2 | AB |, | BN | = 10 cm; | BC | how many cm?

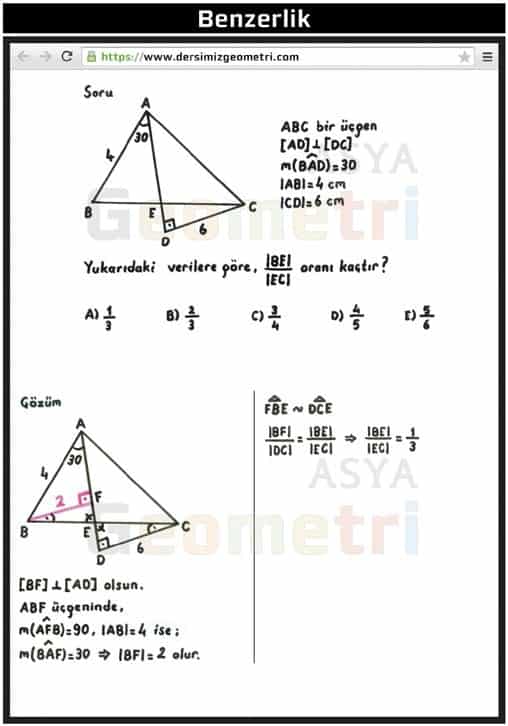
ABC is a triangle, [AD] perpendicular [DC], if m (BAD) = 30 °, | AB | = 4 cm, | CD | = 6 cm; | BE | / | EC | What is the rate?

ABC is a triangle, [AF] and [BF] bisector, [DE] parallel [AB], | AD | = 4 cm, | BE | = 5 cm, | AB | = 12 cm; How many cm is the circumference (DEC)?

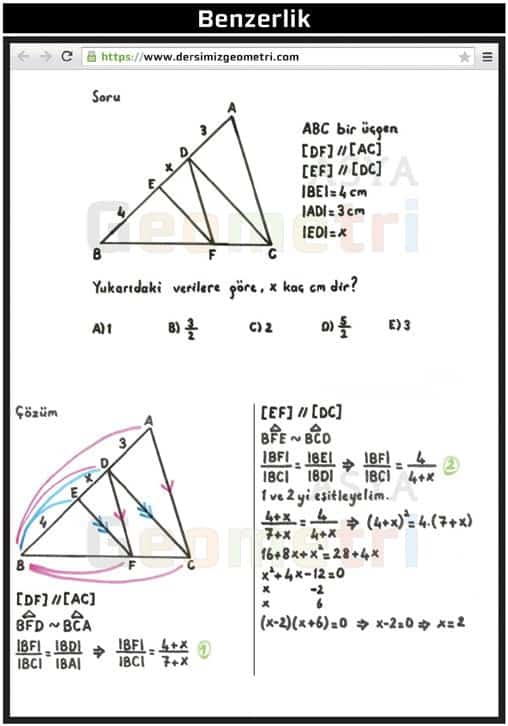
If ABC is a triangle, [DF] parallel [AC], [EF] parallel [DC], | BE | = 4 cm, | AD | = 3 cm; | ED | = how many cm is x?

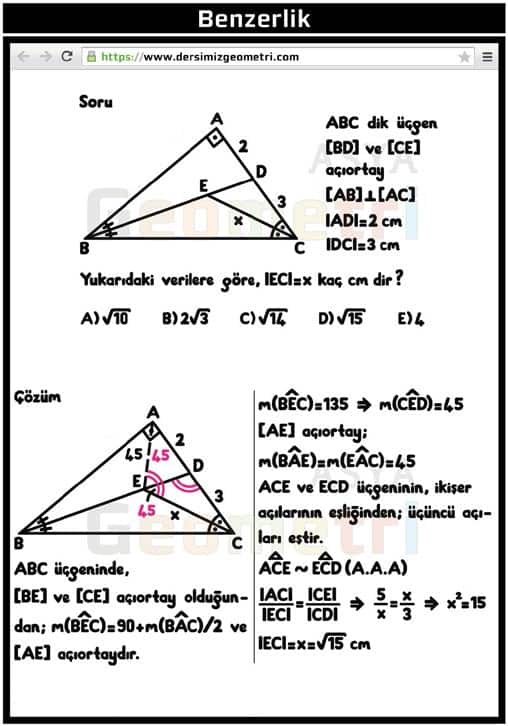
If ABC right triangle, [BD] and [CE] bisector, [AB] right [AC], | AD | = 2 cm, | DC | = 3 cm; | EC | = how many cm is x?

ABC is a right triangle, [AB] perpendicular [AC], [BD] ∩ [EC] = {G}, | BE | = 4 cm, | CD | = 5 cm, If Area (AEGD) = Area (GBC); What is the area of ​​the triangle AED in cm²?

ABC is a right triangle, if [AB] perpendicular [AE], [AC] perpendicular [BC], [BD] ∩ [EC] = {G}, | BD | = 6 cm, | DE | = 4 cm; How many cm² is the area (ABE)?

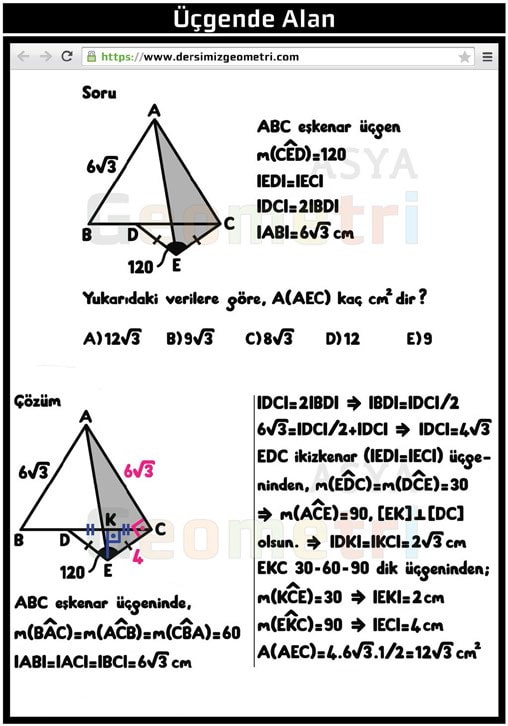
ABC equilateral triangle, if m (CED) = 120 °, | ED | = | EC |, | DC | = 2 | BD |, | AB | = 6 root3 cm; What is the area of ​​the triangle AEC in cm²?

In ABC triangle, if E perpendicular center, A, D, E, F is linear, [BD] perpendicular [DC], Area (BEC) = 8 cm², Area (ABC) = 18 cm²; How many cm² is the area (BDCE)?

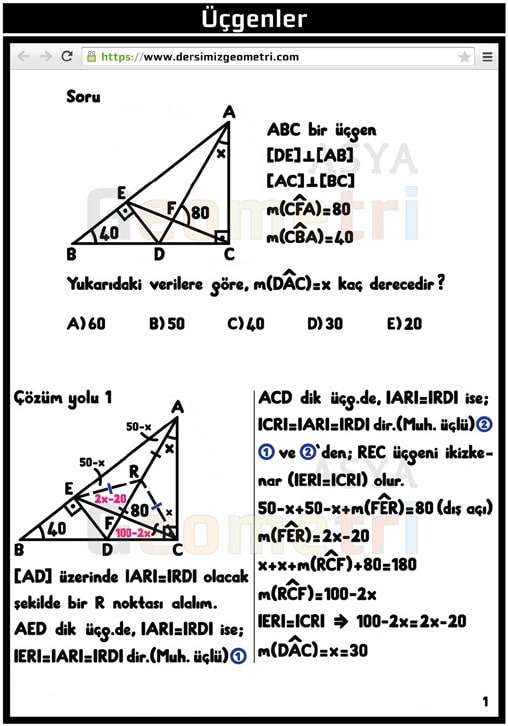
ABC is a triangle, [DE] perpendicular [AB], [AC] perpendicular [BC], if m (CFA) = 80 °, m (CBA) = 40 °; How many degrees is m (DAC) = x?

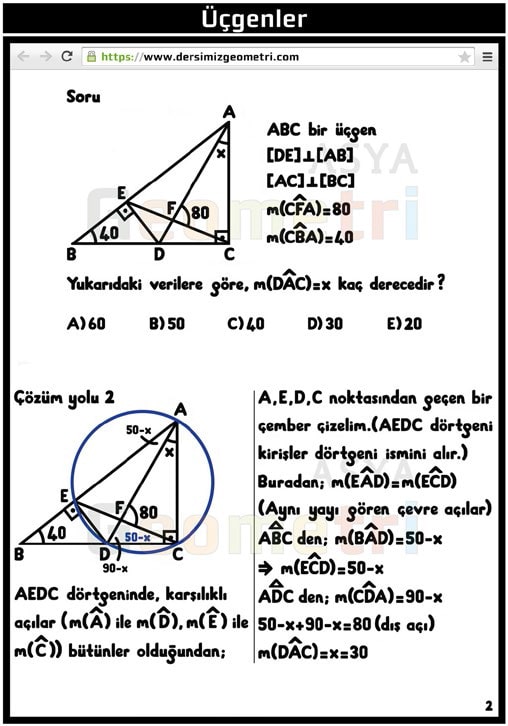
Solution using quadrilateral of beams.

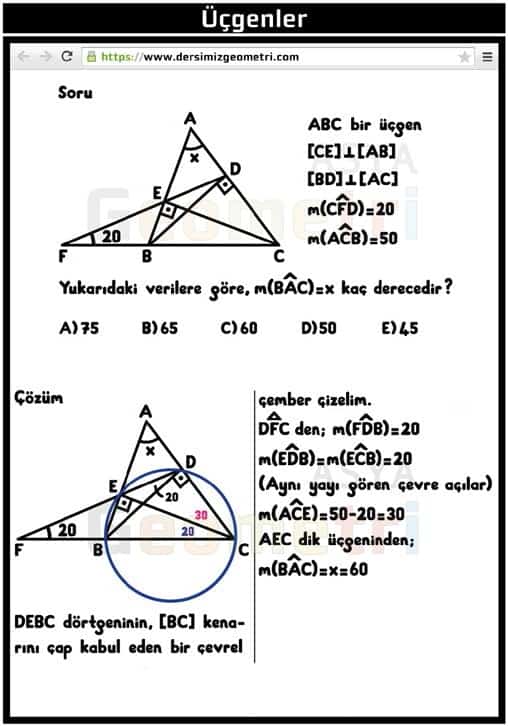
ABC is a triangle, [CE] perpendicular [AB], [BD] perpendicular [AC], if m (CFD) = 20 °, m (ACB) = 50 °; How many degrees is m (BAC) = x?

ABC is a triangle, if | DA | = | DC |, m (BAE) = 10 °, m (DCB) = 20 °, m (DEB) = 80 °; How many degrees is m (AED) = x?

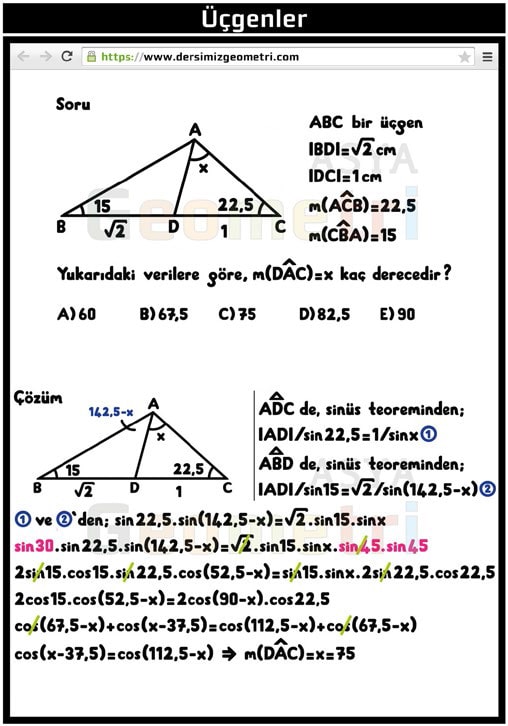
ABC is a triangle, if | BD | = root2 cm, | DC | = 1 cm, m (ACB) = 22.5 °, m (CBA) = 15 °; How many degrees is m (DAC) = x?

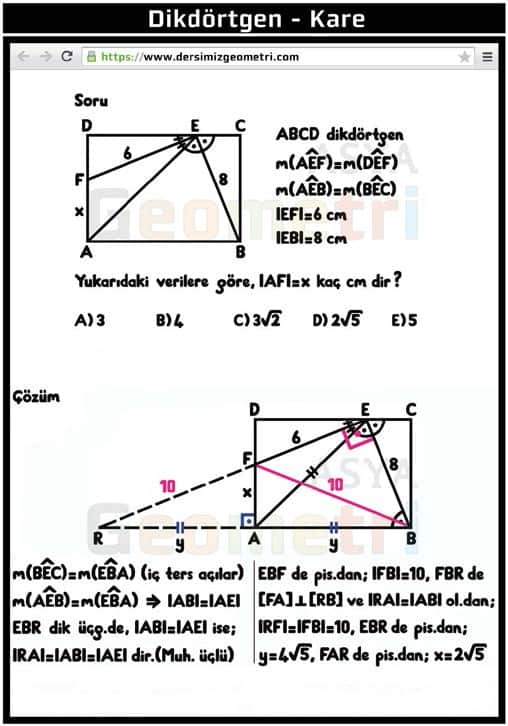
ABCD rectangle, if m (AEF) = m (DEF), m (AEB) = m (BEC), | EF | = 6 cm, | EB | = 8 cm; | AF | = how many cm is x?

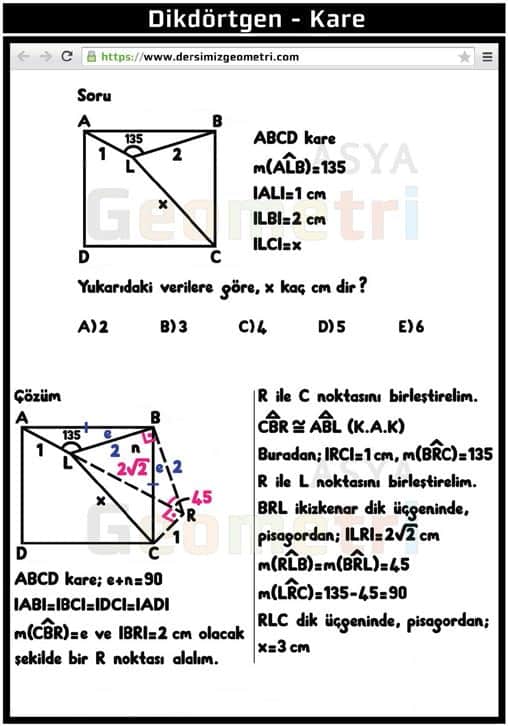
ABC square, if m (ALB) = 135 °, | AL | = 1 cm, | LB | = 2 cm; | LC | = how many cm is x?

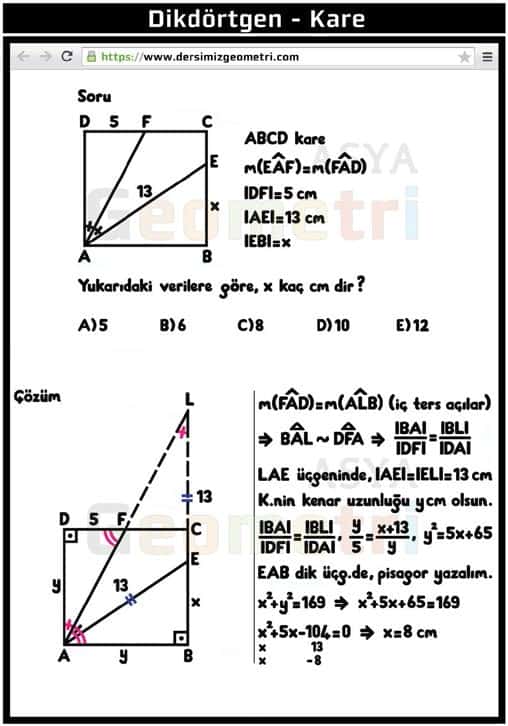
If ABCD square, m (EAF) = m (FAD), | DF | = 5 cm, | AE | = 13 cm; | EB | = how many cm is x?

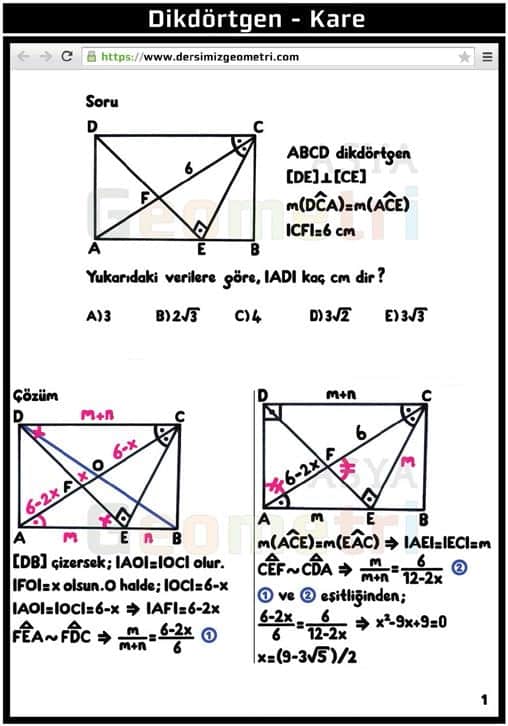
ABCD rectangular, [DE] perpendicular [CE], if m (DCA) = m (ACE), | CF | = 6 cm; | AD | how many cm?

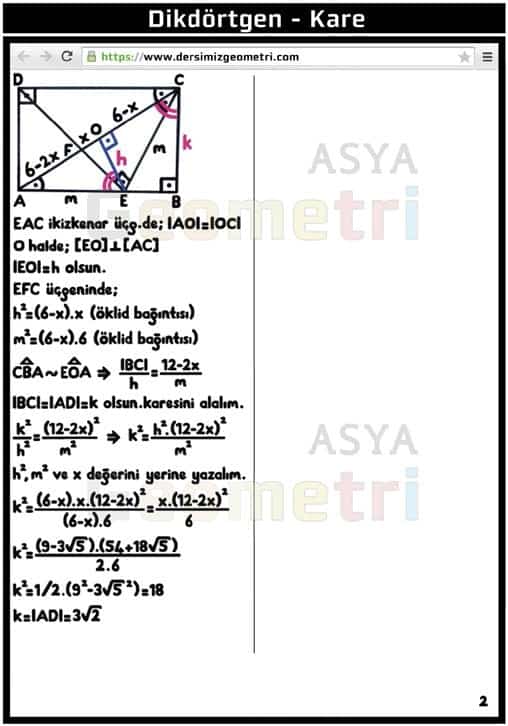
Continuation of the solution to the rectangular question …

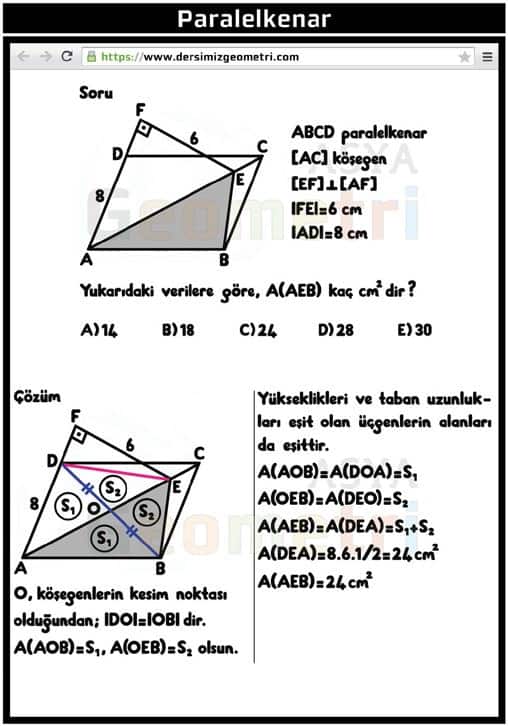
ABCD parallelogram, if [AC] diagonal, [EF] perpendicular [AF], | FE | = 6 cm, | AD | = 8 cm; What is the area of ​​the triangle AEB in cm²?

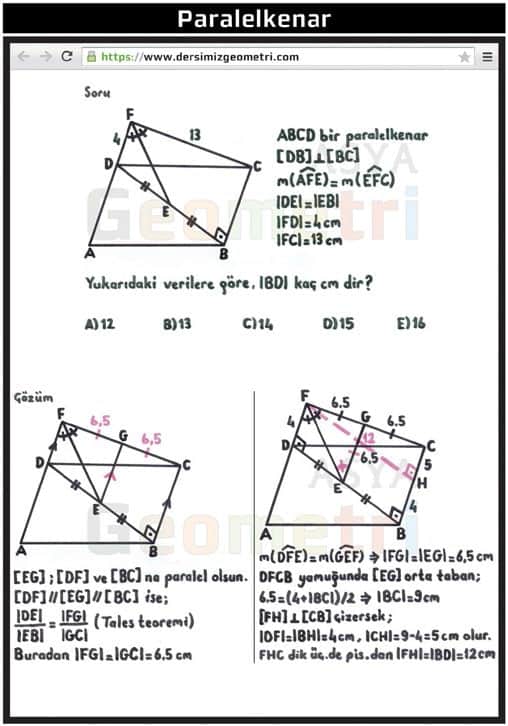
ABCD is a parallelogram, if [DB] perpendicular [BC], m (AFE) = m (EFC), | DE | = | EB |, | FD | = 4 cm, | FC | = 13 cm; | BD | how many cm?

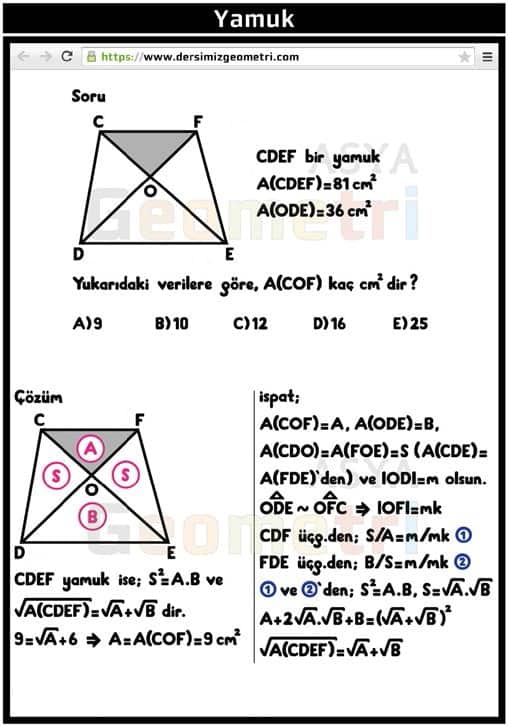
If CDEF is trapezoid, Area (CEDF) = 81 cm², Area (ODE) = 36 cm²; How many cm² is the area (COF)?

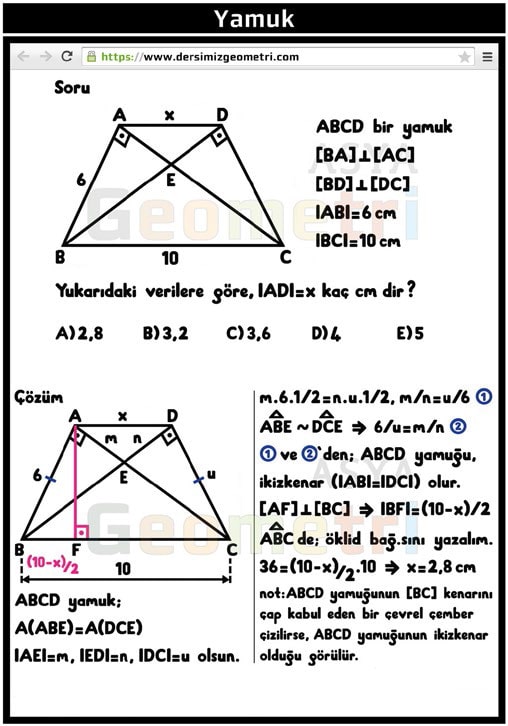
ABCD yamuk, [BA] dik [AC], [BD] dik [DC], |AB|=6 cm, |BC|=10 cm ise; |AD|=x kaç cm dir?

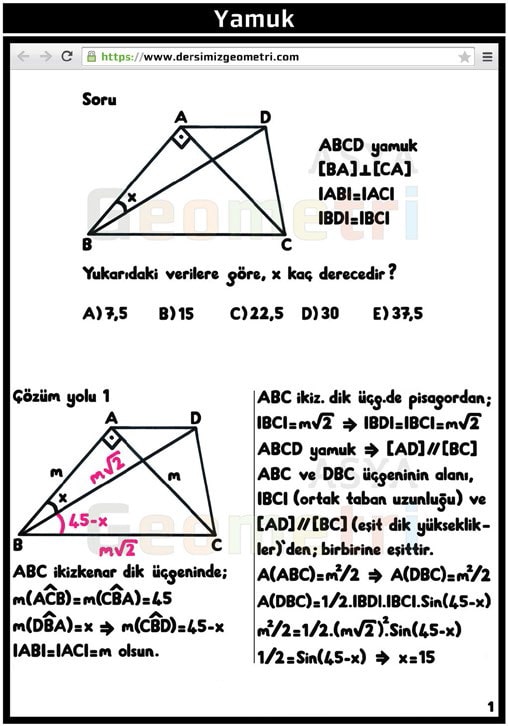
ABCD trapezoid, if [BA] perpendicular [AC], [BD] perpendicular [DC], | AB | = 6 cm, | BC | = 10 cm; | AD | = how many cm is x?

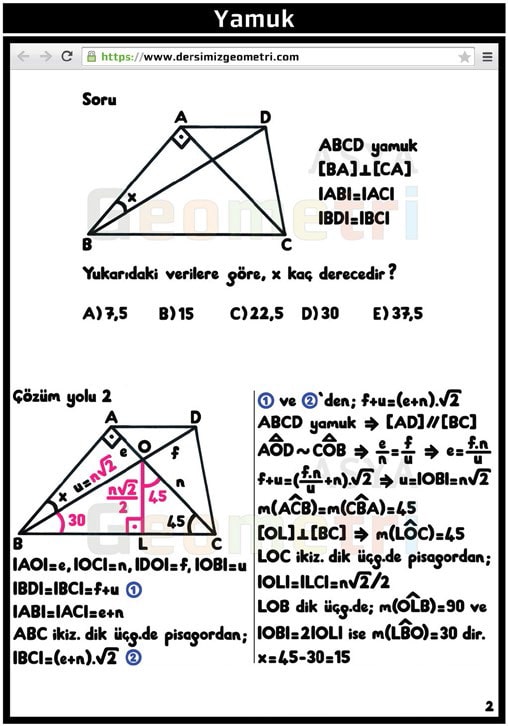
Another solution to the trapezoid problem.

ABC is a triangle, if | AB | = 8 units, | BC | = 6 units, | AC | = 4 units; What is the BA.AC scaler product?

In the orthogonal coordinate system A (0,1), B (3,4), [AB] perpendicular [BC], | AC | if; What is the BC.CA product?

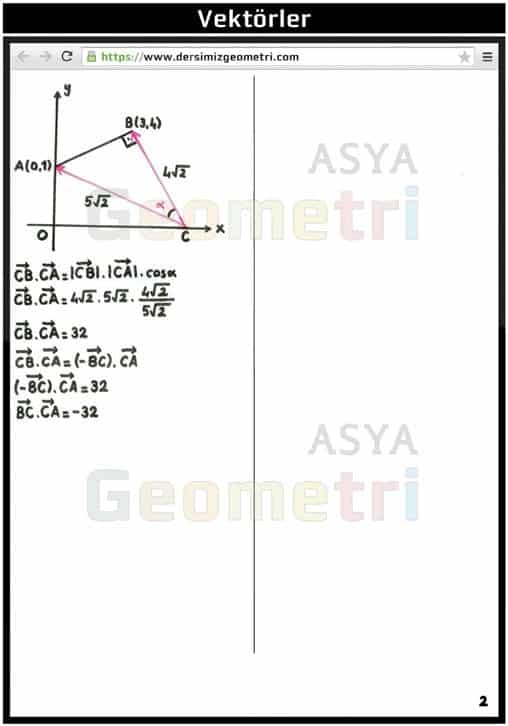
Vectors continuation of the question solution …