
One of thex greatest advantages of working with a geometry tutor is ddthe opportunity for individualized instruction.
The tutor can assess your strengths and weaknesses, identify areas that require additional focus, and tailor the learning process to suit your specific needs.
With personalized attention, you can receive timely feedback on your progress, address misconceptions, and reinforce your understanding of key concepts. This targeted support enables you to maximize your learning potential and make significant strides in geometry.
Geometry is a branch of mathematics that deals with the study of shapes, sizes, and properties of figures and spaces. It plays a crucial role in various fields, including architecture, engineering, physics, and computer graphics.
However, many students find it challenging to grasp the abstract concepts and complex theorems involved. That’s where a geometry tutor can make a world of difference.
In this article, we will explore how a geometry tutor can transform your understanding of this subject, enabling you to excel in geometry and build a solid foundation for future mathematical endeavors.
A geometry tutor has the power to transform your understanding of this intricate branch of mathematics. Through personalized instruction, clear explanations, step-by-step guidance, and ample practice, a tutor can help you navigate the complexities of geometry with ease.
By working closely with a tutor, you can develop a strong foundation in geometry, build problem-solving skills, and gain the confidence necessary to excel in this subject. Embrace the support of a geometry tutor, and unlock the doors to a deeper understanding and appreciation of geometry.
Geometry tutors serve as guides and mentors who help students understand the fundamental principles and concepts of geometry. They provide personalized instruction, catered to the individual needs of the student, which can greatly enhance the learning experience. A geometry tutor can:
Geometry covers a wide range of topics, including:
To excel in geometry, students can employ the following strategies:
Mastering geometry requires a combination of understanding key concepts, practicing problem-solving, and seeking guidance when needed. A geometry tutor can play a vital role in helping students navigate through the intricacies of the subject, providing personalized instruction and support. By following the strategies outlined in this guide and availing the services of a geometry tutor, students can develop a strong foundation in geometry and excel in their academic pursuits.
Free geometry tutoring websites also offer a diverse range of resources to support students’ learning journeys. From interactive lessons and video tutorials to practice problems and quizzes, these websites provide a variety of engaging materials that reinforce understanding and retention of geometry concepts. The interactive nature of these resources enhances student engagement, making the learning process more enjoyable and effective.
One of the key advantages of free geometry tutoring websites is the flexibility they offer in terms of scheduling and learning location. Students can access tutoring sessions from the comfort of their own homes, eliminating the need for travel or fixed schedules.
These websites often provide a range of scheduling options, allowing students to find a time that best fits their availability. This convenience and flexibility enable students to receive geometry tutoring at their own pace and in a stress-free environment.
Additionally, the elimination of financial barriers is a significant advantage of these websites. By offering their services free of charge, they democratize access to high-quality geometry tutoring. Students from all backgrounds can benefit from the expertise of tutors and the resources available, ensuring that no student is left behind due to financial constraints.
There are several reputable free geometry tutoring websites available that you can find through an internet search. Some popular options include Khan Academy (www.khanacademy.org), MathHelp (www.mathhelp.org), and Math Planet (www.mathplanet.org).
When searching for free geometry tutoring websites, make sure to read reviews and check the credibility of the platforms to ensure they meet your specific learning needs.
Online geometry tutoring provides students with personalized instruction tailored to their specific needs. With one-on-one sessions, tutors can assess students’ strengths and weaknesses, identify areas that require additional focus, and create customized lesson plans. This personalized approach ensures that students receive targeted support, allowing them to grasp difficult concepts more effectively.
One of the greatest benefits of online geometry tutoring is the flexibility it offers in terms of scheduling. Students can book tutoring sessions at a time that suits their availability, eliminating the need for fixed schedules or travel time. Whether it’s early morning, late evening, or weekends, online tutoring allows for convenient learning opportunities that can be easily integrated into a student’s routine.
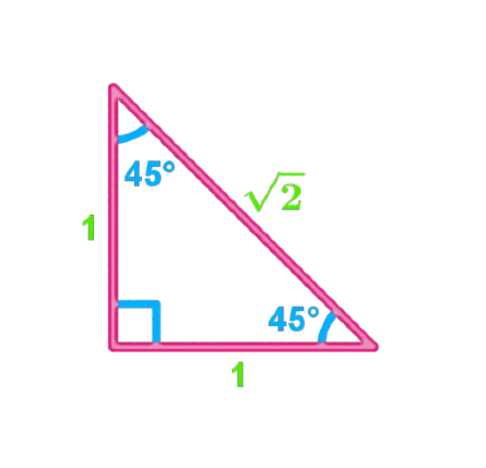
The 45-45-90 triangle gets its name from two equal angles and a right angle. The sides corresponding to both equal angles are of equal length. Therefore, this triangle is an isosceles triangle since both sides of the triangle are the same length. An angle of 90 degrees is called a right angle. Therefore, this triangle is defined as an isosceles right triangle. The 45 45 90 triangle is an important type of triangle, especially used in practical calculation and geometry problems.
The length of the hypotenuse is √2 times the length of the other two sides. So, in a 45 45 90 triangle with two sides of length x, the length of the hypotenuse is x√2.
According to these angles, some properties of the special triangle are as follows:
The 30-60-90 triangle is a special right triangle widely used in trigonometry because it has well-defined relationships between its angles and sides, which can be used to calculate trigonometric functions such as sine, cosine, tangent, and cotangent.
Also known as a “half equilateral triangle,” it gets its name from the fact that if you draw an equilateral triangle and draw an altitude to one of its sides, you will create two 30-60-90 triangles.
Among all the rules, the 30 60 90 triangle rule holds a significant place in geometry. It is valuable in geometry and trigonometry because of its predictable ratios between the lengths of its sides, which can be utilized to solve for unknown values.
The side lengths of this triangle adhere to a specific ratio. The lengths of the sides of a 30-60-90 triangle can be summarized as having a particular relationship, as follows.
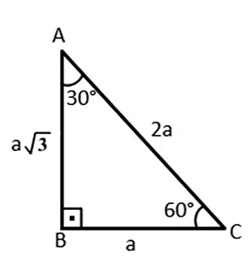
Shortest side = a
Longer side = a√3
Hypotenuse = 2a
Just knowing these ratios will allow us to analyze and practice problem-solving. Therefore, let’s keep these ratios in mind. The values we need to know are 1, √3, and 2.
In a right triangle, if the length of the side opposite the 30-degree angle is 6 cm, what are the lengths of the other sides?
The hypotenuse is twice the length of the side opposite the 30-degree angle, so it is 2 * 6 = 12 cm.
The side opposite the 60-degree angle is √3 times the length of the side opposite the 30-degree angle, so it is 6 * √3 = 6√3 cm. Alternatively, since it is (√3)/2 times the length of the hypotenuse, it is again 12 * (√3)/2 = 6√3 cm.
Therefore, the sides of this 30-60-90 triangle are 6 cm, 6√3 cm, and 12 cm.
We can extend the examples of the 30-60-90 triangle. You can find 30-60-90 triangle questions and answers in the “Right Triangles” category under triangle tests.
In conclusion, if you know the length of one side, you can use these ratios to find the lengths of the other two sides.
If we know the lengths of any two sides…
Yes, we can use these ratios again to find the length of the third side. Alternatively, we can use the Pythagorean theorem, which states that in a right triangle, the sum of the squares of the two legs is equal to the square of the hypotenuse.
We know the ratios, but we got confused about whether it was √3 times the side opposite the 30-degree angle or the side opposite the 60-degree angle…
What should we do?
Let’s draw the 30-60-90 triangle.
Immediately, we write down “1” for the length of the side opposite the 30-degree angle because it is the shortest side.
Then, we ask ourselves if it’s 2 or √3. If √3 were equal to √4, we would take the value of 2, so we say it’s 2…
Since 2 is the largest, we can write “2” for the side opposite the 90-degree angle, and consequently, “√3” for the third side, which is the side opposite the 60-degree angle.
But what if we don’t know the rule…?
We will examine the importance of the Sin(30) value in determining the ratios between the short side, long side, and hypotenuse in the 30-60-90 triangle. Trigonometry emerges as a branch that plays an important role in geometry and mathematics. Particularly, the use of trigonometric functions in triangles allows us to understand the relationship between angles and side lengths.
The sine function represents the ratio of the side opposite an angle to the hypotenuse. The value of Sin(30) holds significance in the analysis of special triangles like the 30-60-90 triangle and in geometric calculations. This is where Sin(30) comes into play.
The value of the sine of the 30-degree angle, mathematically expressed as Sin(30), is equal to 1/2. This means that the short side will be half the length of the hypotenuse.
Therefore, in the 30-60-90 triangle, the length of the hypotenuse is twice the length of the side opposite the 30-degree angle.
In conclusion, it demonstrates the significant role of trigonometric functions, specifically sine values, in determining the ratios in the lengths of the sides of a triangle.
Let’s draw a 30°-60°-90° triangle.
Since sin30° is equal to the ratio of the side opposite the angle to the hypotenuse, we can determine the ratio between the side opposite the 30° angle and the hypotenuse as 1:2. As for the side opposite the 60° angle, we can determine its ratio by either using sin60° or the Pythagorean theorem, which would be √3.
Here, in the 30-60-90 triangle, the most important thing is to either know the rule or apply the trigonometric function.
But what if we have no idea…

In an equilateral triangle, we draw a perpendicular to any side. Since the perpendicular acts as the median, angle bisector, and altitude, it divides the side into two equal lengths. Therefore, we observe a ratio of 1:2. By using the Pythagorean theorem, we can also determine that the third side has the ratios of Shortest side = a, Longer side = a√3, Hypotenuse = 2a in the 30-60-90 triangle..
The properties and applications of the 30-60-90 triangle make it a valuable tool in solving geometric problems and designing real-world structures. It finds practical applications in fields such as engineering, architecture, and construction. For example, it can be used to design and construct ramps, stairs, and other structures with gradual slopes.

The most important thing to study geometry is to be enthusiastic and to deal with it from your heart.
Geometry lesson is a lesson that students generally have difficulty with. With regular practice, you can definitely be successful.
It is based on a few basic concepts, theorems and axioms. Subsequent new theorems are also used as auxiliary ones.
When they are added to each other like the links of a chain, they turn into a new state, that is relations. Therefore, it is important to know the basic geometric concepts while studying.
You should listen carefully to your geometry teacher in class. In the lecture, your teacher writes the relevant formulas based on their previous lectures. Each new formula is related to the topics you see. If you miss a topic, you may find it difficult to understand the next topic.
Understand the basic concepts: Geometry builds on basic concepts such as points, lines, angles, and shapes. Make sure you have a strong understanding of these concepts before moving on to more complex topics.
Practice, practice, practice: Geometry requires a lot of practice to master. Do as many problems as you can and try to work through them on your own before seeking help.
Draw diagrams: Geometry is a visual subject, so drawing diagrams can be very helpful in understanding concepts and solving problems.
Use textbooks and other resources: Use textbooks, online resources, and other materials to supplement your classroom learning. These resources can provide additional explanations and practice problems.
Work with others: Working with classmates or a tutor can be helpful in understanding difficult concepts and getting feedback on your work.
To study regulary and planned: Regular review can help you retain information and identify areas that need more practice. If you want to be successful in geometry, you must study regularly. You must learn the lesson in class. After the lecture, your teacher should go step by step while solving many geometry questions and arouse your curiosity. You must be able to fully understand what is being taught in class.
It would be wrong to say that you have to solve so many geometry questions a day. Because when we think that everyone has a different understanding ability, it would not be right to give a question or time limit.
Stay organized: Keep your notes and assignments organized and up-to-date. This can help you stay on top of your work and avoid falling behind.
Overall, studying geometry requires a combination of understanding basic concepts, practice, and using resources to supplement your learning. By following these tips, you can improve your understanding of geometry and achieve success in your studies.

The trigonometric table contains the calculated values of the trigonometric functions for a given angle from 0 to 360 degrees.
Calculator techniques for problems related to circles and triangles are more on algebra, trigonometry and geometry.
Trigonometry studies the relationship between the angles and lengths of a triangle.
In a right triangle, there are six different ratios that we can write between the three sides of the unit circle. Each of them is a function. Trigonometric functions are 4 as sine, cosine, tangent and cotengent, and 2 as secant and cosecant subfunctions obtained from these functions.
By using trigonometric functions and formulas table, many geometric calculations such as angle-side connections of triangles, finding interior angles, relations with neighboring angles can be done easily.
Trigonometry is a key area of mathematics that examines the relationships between angles and sides of triangles. Knowing the trigonometric values of special angles can be very helpful in many applications. Here are the sine, cosine, tangent, and cotangent values for the angles 0°, 30°, 45°, 60°, and 90°:
In a right triangle, the cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. For special angles:
In a right triangle, the cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. For special angles:
In a right triangle, the tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side. For special angles:
In a right triangle, the cotangent of an angle is the reciprocal of the tangent. It is the ratio of the length of the adjacent side to the length of the opposite side. For special angles:
These values are crucial not only in math but also in physics, engineering, and other sciences. They help in understanding concepts like circular motion and waves.
By memorizing these values, you can solve problems more easily and grasp more complex mathematical ideas. A solid understanding of these fundamental trigonometric values can greatly enhance your math skills.
The trigonometric values table from 0 to 360 lists the one-degree increment values of the sine (sin), cosine (cos), tangent (tan), cotangent (cot) functions.
Sine 0 = 0.0
Cosine 0 = 1.0
Tangent 0 = 0.0
Cotangent 0 = ∞
Sine 1 = 0.0174524064373
Cosine 1 = 0.999847695156
Tangent 1 = 0.0174550649282
Cotangent 1 = 57.2899616308
Sine 2 = 0.0348994967025
Cosine 2 = 0.999390827019
Tangent 2 = 0.0349207694917
Cotangent 2 = 28.6362532829
Sine 3 = 0.0523359562429
Cosine 3 = 0.998629534755
Tangent 3 = 0.052407779283
Cotangent 3 = 19.0811366877
Sine 4 = 0.0697564737441
Cosine 4 = 0.99756405026
Tangent 4 = 0.0699268119435
Cotangent 4 = 14.3006662567
Sine 5 = 0.0871557427477
Cosine 5 = 0.996194698092
Tangent 5 = 0.0874886635259
Cotangent 5 = 11.4300523028
Sine 6 = 0.104528463268
Cosine 6 = 0.994521895368
Tangent 6 = 0.105104235266
Cotangent 6 = 9.51436445422
Sine 7 = 0.121869343405
Cosine 7 = 0.992546151641
Tangent 7 = 0.122784560903
Cotangent 7 = 8.14434642797
Sine 8 = 0.13917310096
Cosine 8 = 0.990268068742
Tangent 8 = 0.140540834702
Cotangent 8 = 7.11536972238
Sine 9 = 0.15643446504
Cosine 9 = 0.987688340595
Tangent 9 = 0.158384440325
Cotangent 9 = 6.31375151468
Sine 10 = 0.173648177667
Cosine 10 = 0.984807753012
Tangent 10 = 0.176326980708
Cotangent 10 = 5.67128181962
Sine 11 = 0.190808995377
Cosine 11 = 0.981627183448
Tangent 11 = 0.194380309138
Cotangent 11 = 5.14455401597
Sine 12 = 0.207911690818
Cosine 12 = 0.978147600734
Tangent 12 = 0.21255656167
Cotangent 12 = 4.70463010948
Sine 13 = 0.224951054344
Cosine 13 = 0.974370064785
Tangent 13 = 0.230868191126
Cotangent 13 = 4.33147587428
Sine 14 = 0.2419218956
Cosine 14 = 0.970295726276
Tangent 14 = 0.249328002843
Cotangent 14 = 4.01078093354
Sine 15 = 0.258819045103
Cosine 15 = 0.965925826289
Tangent 15 = 0.267949192431
Cotangent 15 = 3.73205080757
Sine 16 = 0.275637355817
Cosine 16 = 0.961261695938
Tangent 16 = 0.286745385759
Cotangent 16 = 3.48741444384
Sine 17 = 0.292371704723
Cosine 17 = 0.956304755963
Tangent 17 = 0.305730681459
Cotangent 17 = 3.27085261848
Sine 18 = 0.309016994375
Cosine 18 = 0.951056516295
Tangent 18 = 0.324919696233
Cotangent 18 = 3.07768353718
Sine 19 = 0.325568154457
Cosine 19 = 0.945518575599
Tangent 19 = 0.34432761329
Cotangent 19 = 2.90421087768
Sine 20 = 0.342020143326
Cosine 20 = 0.939692620786
Tangent 20 = 0.363970234266
Cotangent 20 = 2.74747741945
Sine 21 = 0.358367949545
Cosine 21 = 0.933580426497
Tangent 21 = 0.383864035035
Cotangent 21 = 2.60508906469
Sine 22 = 0.374606593416
Cosine 22 = 0.927183854567
Tangent 22 = 0.404026225835
Cotangent 22 = 2.47508685342
Sine 23 = 0.390731128489
Cosine 23 = 0.920504853452
Tangent 23 = 0.42447481621
Cotangent 23 = 2.35585236582
Sine 24 = 0.406736643076
Cosine 24 = 0.913545457643
Tangent 24 = 0.445228685309
Cotangent 24 = 2.2460367739
Sine 25 = 0.422618261741
Cosine 25 = 0.906307787037
Tangent 25 = 0.466307658155
Cotangent 25 = 2.14450692051
Sine 26 = 0.438371146789
Cosine 26 = 0.898794046299
Tangent 26 = 0.487732588566
Cotangent 26 = 2.05030384158
Sine 27 = 0.45399049974
Cosine 27 = 0.891006524188
Tangent 27 = 0.509525449494
Cotangent 27 = 1.96261050551
Sine 28 = 0.469471562786
Cosine 28 = 0.882947592859
Tangent 28 = 0.531709431661
Cotangent 28 = 1.88072646535
Sine 29 = 0.484809620246
Cosine 29 = 0.874619707139
Tangent 29 = 0.554309051453
Cotangent 29 = 1.80404775527
Sine 30 = 0.5
Cosine 30 = 0.866025403784
Tangent 30 = 0.57735026919
Cotangent 30 = 1.73205080757
Sine 31 = 0.51503807491
Cosine 31 = 0.857167300702
Tangent 31 = 0.600860619028
Cotangent 31 = 1.66427948235
Sine 32 = 0.529919264233
Cosine 32 = 0.848048096156
Tangent 32 = 0.624869351909
Cotangent 32 = 1.60033452904
Sine 33 = 0.544639035015
Cosine 33 = 0.838670567945
Tangent 33 = 0.649407593198
Cotangent 33 = 1.53986496381
Sine 34 = 0.559192903471
Cosine 34 = 0.829037572555
Tangent 34 = 0.674508516842
Cotangent 34 = 1.48256096851
Sine 35 = 0.573576436351
Cosine 35 = 0.819152044289
Tangent 35 = 0.70020753821
Cotangent 35 = 1.42814800674
Sine 36 = 0.587785252292
Cosine 36 = 0.809016994375
Tangent 36 = 0.726542528005
Cotangent 36 = 1.37638192047
Sine 37 = 0.601815023152
Cosine 37 = 0.798635510047
Tangent 37 = 0.753554050103
Cotangent 37 = 1.32704482162
Sine 38 = 0.615661475326
Cosine 38 = 0.788010753607
Tangent 38 = 0.781285626507
Cotangent 38 = 1.27994163219
Sine 39 = 0.62932039105
Cosine 39 = 0.777145961457
Tangent 39 = 0.809784033195
Cotangent 39 = 1.23489715654
Sine 40 = 0.642787609687
Cosine 40 = 0.766044443119
Tangent 40 = 0.839099631177
Cotangent 40 = 1.19175359259
Sine 41 = 0.656059028991
Cosine 41 = 0.754709580223
Tangent 41 = 0.869286737816
Cotangent 41 = 1.15036840722
Sine 42 = 0.669130606359
Cosine 42 = 0.743144825477
Tangent 42 = 0.900404044298
Cotangent 42 = 1.11061251483
Sine 43 = 0.681998360062
Cosine 43 = 0.731353701619
Tangent 43 = 0.932515086138
Cotangent 43 = 1.07236871002
Sine 44 = 0.694658370459
Cosine 44 = 0.719339800339
Tangent 44 = 0.965688774807
Cotangent 44 = 1.03553031379
Sine 45 = 0.707106781187
Cosine 45 = 0.707106781187
Tangent 45 = 1.0
Cotangent 45 = 1.0
Sine 46 = 0.719339800339
Cosine 46 = 0.694658370459
Tangent 46 = 1.03553031379
Cotangent 46 = 0.965688774807
Sine 47 = 0.731353701619
Cosine 47 = 0.681998360062
Tangent 47 = 1.07236871002
Cotangent 47 = 0.932515086138
Sine 48 = 0.743144825477
Cosine 48 = 0.669130606359
Tangent 48 = 1.11061251483
Cotangent 48 = 0.900404044298
Sine 49 = 0.754709580223
Cosine 49 = 0.656059028991
Tangent 49 = 1.15036840722
Cotangent 49 = 0.869286737816
Sine 50 = 0.766044443119
Cosine 50 = 0.642787609687
Tangent 50 = 1.19175359259
Cotangent 50 = 0.839099631177
Sine 51 = 0.777145961457
Cosine 51 = 0.62932039105
Tangent 51 = 1.23489715654
Cotangent 51 = 0.809784033195
Sine 52 = 0.788010753607
Cosine 52 = 0.615661475326
Tangent 52 = 1.27994163219
Cotangent 52 = 0.781285626507
Sine 53 = 0.798635510047
Cosine 53 = 0.601815023152
Tangent 53 = 1.32704482162
Cotangent 53 = 0.753554050103
Sine 54 = 0.809016994375
Cosine 54 = 0.587785252292
Tangent 54 = 1.37638192047
Cotangent 54 = 0.726542528005
Sine 55 = 0.819152044289
Cosine 55 = 0.573576436351
Tangent 55 = 1.42814800674
Cotangent 55 = 0.70020753821
Sine 56 = 0.829037572555
Cosine 56 = 0.559192903471
Tangent 56 = 1.48256096851
Cotangent 56 = 0.674508516842
Sine 57 = 0.838670567945
Cosine 57 = 0.544639035015
Tangent 57 = 1.53986496381
Cotangent 57 = 0.649407593198
Sine 58 = 0.848048096156
Cosine 58 = 0.529919264233
Tangent 58 = 1.60033452904
Cotangent 58 = 0.624869351909
Sine 59 = 0.857167300702
Cosine 59 = 0.51503807491
Tangent 59 = 1.66427948235
Cotangent 59 = 0.600860619028
Sine 60 = 0.866025403784
Cosine 60 = 0.5
Tangent 60 = 1.73205080757
Cotangent 60 = 0.57735026919
Sine 61 = 0.874619707139
Cosine 61 = 0.484809620246
Tangent 61 = 1.80404775527
Cotangent 61 = 0.554309051453
Sine 62 = 0.882947592859
Cosine 62 = 0.469471562786
Tangent 62 = 1.88072646535
Cotangent 62 = 0.531709431661
Sine 63 = 0.891006524188
Cosine 63 = 0.45399049974
Tangent 63 = 1.96261050551
Cotangent 63 = 0.509525449494
Sine 64 = 0.898794046299
Cosine 64 = 0.438371146789
Tangent 64 = 2.05030384158
Cotangent 64 = 0.487732588566
Sine 65 = 0.906307787037
Cosine 65 = 0.422618261741
Tangent 65 = 2.14450692051
Cotangent 65 = 0.466307658155
Sine 66 = 0.913545457643
Cosine 66 = 0.406736643076
Tangent 66 = 2.2460367739
Cotangent 66 = 0.445228685309
Sine 67 = 0.920504853452
Cosine 67 = 0.390731128489
Tangent 67 = 2.35585236582
Cotangent 67 = 0.42447481621
Sine 68 = 0.927183854567
Cosine 68 = 0.374606593416
Tangent 68 = 2.47508685342
Cotangent 68 = 0.404026225835
Sine 69 = 0.933580426497
Cosine 69 = 0.358367949545
Tangent 69 = 2.60508906469
Cotangent 69 = 0.383864035035
Sine 70 = 0.939692620786
Cosine 70 = 0.342020143326
Tangent 70 = 2.74747741945
Cotangent 70 = 0.363970234266
Sine 71 = 0.945518575599
Cosine 71 = 0.325568154457
Tangent 71 = 2.90421087768
Cotangent 71 = 0.34432761329
Sine 72 = 0.951056516295
Cosine 72 = 0.309016994375
Tangent 72 = 3.07768353718
Cotangent 72 = 0.324919696233
Sine 73 = 0.956304755963
Cosine 73 = 0.292371704723
Tangent 73 = 3.27085261848
Cotangent 73 = 0.305730681459
Sine 74 = 0.961261695938
Cosine 74 = 0.275637355817
Tangent 74 = 3.48741444384
Cotangent 74 = 0.286745385759
Sine 75 = 0.965925826289
Cosine 75 = 0.258819045103
Tangent 75 = 3.73205080757
Cotangent 75 = 0.267949192431
Sine 76 = 0.970295726276
Cosine 76 = 0.2419218956
Tangent 76 = 4.01078093354
Cotangent 76 = 0.249328002843
Sine 77 = 0.974370064785
Cosine 77 = 0.224951054344
Tangent 77 = 4.33147587428
Cotangent 77 = 0.230868191126
Sine 78 = 0.978147600734
Cosine 78 = 0.207911690818
Tangent 78 = 4.70463010948
Cotangent 78 = 0.21255656167
Sine 79 = 0.981627183448
Cosine 79 = 0.190808995377
Tangent 79 = 5.1445401597
Cotangent 79 = 0.194380309138
Sine 80 = 0.984807753012
Cosine 80 = 0.173648177667
Tangent 80 = 5.67128181962
Cotangent 80 = 0.176326980708
Sine 81 = 0.987688340595
Cosine 81 = 0.15643446504
Tangent 81 = 6.31375151468
Cotangent 81 = 0.158384440325
Sine 82 = 0.990268068742
Cosine 82 = 0.13917310096
Tangent 82 = 7.11536972238
Cotangent 82 = 0.140540834702
Sine 83 = 0.992546151641
Cosine 83 = 0.121869343405
Tangent 83 = 8.14434642797
Cotangent 83 = 0.122784560903
Sine 84 = 0.994521895368
Cosine 84 = 0.104528463268
Tangent 84 = 9.51436445422
Cotangent 84 = 0.105104235266
Sine 85 = 0.996194698092
Cosine 85 = 0.0871557427477
Tangent 85 = 11.4300523028
Cotangent 85 = 0.0874886635259
Sine 86 = 0.99756405026
Cosine 86 = 0.0697564737441
Tangent 86 = 14.3006662567
Cotangent 86 = 0.0699268119435
Sine 87 = 0.998629534755
Cosine 87 = 0.0523359562429
Tangent 87 = 19.0811366877
Cotangent 87 = 0.052407779283
Sine 88 = 0.999390827019
Cosine 88 = 0.0348994967025
Tangent 88 = 28.6362532829
Cotangent 88 = 0.0349207694917
Sine 89 = 0.999847695156
Cosine 89 = 0.0174524064373
Tangent 89 = 57.2899616308
Cotangent 89 = 0.0174550649282
Sine 90 = 1.0
Cosine 90 = 0.0
Tangent 90= ∞
Cotangent 90 = 0.0
Sine 91 = 0.999847695156
Cosine 91 = -0.0174524064373
Tangent 91 = -57.2899616308
Cotangent 91 = -0.0174550649282
Sine 92 = 0.999390827019
Cosine 92 = -0.0348994967025
Tangent 92 = -28.6362532829
Cotangent 92 = -0.0349207694917
Sine 93 = 0.998629534755
Cosine 93 = -0.0523359562429
Tangent 93 = -19.0811366877
Cotangent 93 = -0.052407779283
Sine 94 = 0.99756405026
Cosine 94 = -0.0697564737441
Tangent 94 = -14.3006662567
Cotangent 94 = -0.0699268119435
Sine 95 = 0.996194698092
Cosine 95 = -0.0871557427477
Tangent 95 = -11.4300523028
Cotangent 95 = -0.0874886635259
Sine 96 = 0.994521895368
Cosine 96 = -0.104528463268
Tangent 96 = -9.51436445422
Cotangent 96 = -0.105104235266
Sine 97 = 0.992546151641
Cosine 97 = -0.121869343405
Tangent 97 = -8.14434642797
Cotangent 97 = -0.122784560903
Sine 98 = 0.990268068742
Cosine 98 = -0.13917310096
Tangent 98 = -7.11536972238
Cotangent 98 = -0.140540834702
Sine 99 = 0.987688340595
Cosine 99 = -0.15643446504
Tangent 99 = -6.31375151468
Cotangent 99 = -0.158384440325
Sine 100 = 0.984807753012
Cosine 100 = -0.173648177667
Tangent 100 = -5.67128181962
Cotangent 100 = -0.176326980708
Sine 101 = 0.981627183448
Cosine 101 = -0.190808995377
Tangent 101 = -5.14455401597
Cotangent 101 = -0.194380309138
Sine 102 = 0.978147600734
Cosine 102 = -0.207911690818
Tangent 102 = -4.70463010948
Cotangent 102 = -0.21255656167
Sine 103 = 0.974370064785
Cosine 103 = -0.224951054344
Tangent 103 = -4.33147587428
Cotangent 103 = -0.230868191126
Sine 104 = 0.970295726276
Cosine 104 = -0.2419218956
Tangent 104 = -4.01078093354
Cotangent 104 = -0.249328002843
Sine 105 = 0.965925826289
Cosine 105 = -0.258819045103
Tangent 105 = -3.73205080757
Cotangent 105 = -0.267949192431
Sine 106 = 0.961261695938
Cosine 106 = -0.275637355817
Tangent 106 = -3.48741444384
Cotangent 106 = -0.286745385759
Sine 107 = 0.956304755963
Cosine 107 = -0.292371704723
Tangent 107 = -3.27085261848
Cotangent 107 = -0.305730681459
Sine 108 = 0.951056516295
Cosine 108 = -0.309016994375
Tangent 108 = -3.07768353718
Cotangent 108 = -0.324919696233
Sine 109 = 0.945518575599
Cosine 109 = -0.325568154457
Tangent 109 = -2.90421087768
Cotangent 109 = -0.34432761329
Sine 110 = 0.939692620786
Cosine 110 = -0.342020143326
Tangent 110 = -2.74747741945
Cotangent 110 = -0.363970234266
Sine 111 = 0.933580426497
Cosine 111 = -0.358367949545
Tangent 111 = -2.60508906469
Cotangent 111 = -0.383864035035
Sine 112 = 0.927183854567
Cosine 112 = -0.374606593416
Tangent 112 = -2.47508685342
Cotangent 112 = -0.404026225835
Sine 113 = 0.920504853452
Cosine 113 = -0.390731128489
Tangent 113 = -2.35585236582
Cotangent 113 = -0.42447481621
Sine 114 = 0.913545457643
Cosine 114 = -0.406736643076
Tangent 114 = -2.2460367739
Cotangent 114 = -0.445228685309
Sine 115 = 0.906307787037
Cosine 115 = -0.422618261741
Tangent 115 = -2.14450692051
Cotangent 115 = -0.466307658155
Sine 116 = 0.898794046299
Cosine 116 = -0.438371146789
Tangent 116 = -2.05030384158
Cotangent 116 = -0.487732588566
Sine 117 = 0.891006524188
Cosine 117 = -0.45399049974
Tangent 117 = -1.96261050551
Cotangent 117 = -0.509525449494
Sine 118 = 0.882947592859
Cosine 118 = -0.469471562786
Tangent 118 = -1.88072646535
Cotangent 118 = -0.531709431661
Sine 119 = 0.874619707139
Cosine 119 = -0.484809620246
Tangent 119 = -1.80404775527
Cotangent 119 = -0.554309051453
Sine 120 = 0.866025403784
Cosine 120 = -0.5
Tangent 120 = -1.73205080757
Cotangent 120 = -0.57735026919
Sine 121 = 0.857167300702
Cosine 121 = -0.51503807491
Tangent 121 = -1.66427948235
Cotangent 121 = -0.600860619028
Sine 122 = 0.848048096156
Cosine 122 = -0.529919264233
Tangent 122 = -1.60033452904
Cotangent 122 = -0.624869351909
Sine 123 = 0.838670567945
Cosine 123 = -0.544639035015
Tangent 123 = -1.53986496381
Cotangent 123 = -0.649407593198
Sine 124 = 0.829037572555
Cosine 124 = -0.559192903471
Tangent 124 = -1.48256096851
Cotangent 124 = -0.674508516842
Sine 125 = 0.819152044289
Cosine 125 = -0.573576436351
Tangent 125 = -1.42814800674
Cotangent 125 = -0.70020753821
Sine 126 = 0.809016994375
Cosine 126 = -0.587785252292
Tangent 126 = -1.37638192047
Cotangent 126 = -0.726542528005
Sine 127 = 0.798635510047
Cosine 127 = -0.601815023152
Tangent 127 = -1.32704482162
Cotangent 127 = -0.753554050103
Sine 128 = 0.788010753607
Cosine 128 = -0.615661475326
Tangent 128 = -1.27994163219
Cotangent 128 = -0.781285626507
Sine 129 = 0.777145961457
Cosine 129 = -0.62932039105
Tangent 129 = -1.23489715654
Cotangent 129 = -0.809784033195
Sine 130 = 0.766044443119
Cosine 130 = -0.642787609687
Tangent 130 = -1.19175359259
Cotangent 130 = -0.839099631177
Sine 131 = 0.754709580223
Cosine 131 = -0.656059028991
Tangent 131 = -1.15036840722
Cotangent 131 = -0.869286737816
Sine 132 = 0.743144825477
Cosine 132 = -0.669130606359
Tangent 132 = -1.11061251483
Cotangent 132 = -0.900404044298
Sine 133 = 0.731353701619
Cosine 133 = -0.681998360062
Tangent 133 = -1.07236871002
Cotangent 133 = -0.932515086138
Sine 134 = 0.719339800339
Cosine 134 = -0.694658370459
Tangent 134 = -1.03553031379
Cotangent 134 = -0.965688774807
Sine 135 = 0.707106781187
Cosine 135 = -0.707106781187
Tangent 135 = -1.0
Cotangent 135 = -1.0
Sine 136 = 0.694658370459
Cosine 136 = -0.719339800339
Tangent 136 = -0.965688774807
Cotangent 136 = -1.03553031379
Sine 137 = 0.681998360062
Cosine 137 = -0.731353701619
Tangent 137 = -0.932515086138
Cotangent 137 = -1.07236871002
Sine 138 = 0.669130606359
Cosine 138 = -0.743144825477
Tangent 138 = -0.900404044298
Cotangent 138 = -1.11061251483
Sine 139 = 0.656059028991
Cosine 139 = -0.754709580223
Tangent 139 = -0.869286737816
Cotangent 139 = -1.15036840722
Sine 140 = 0.642787609687
Cosine 140 = -0.766044443119
Tangent 140 = -0.839099631177
Cotangent 140 = -1.19175359259
Sine 141 = 0.62932039105
Cosine 141 = -0.777145961457
Tangent 141 = -0.809784033195
Cotangent 141 = -1.23489715654
Sine 142 = 0.615661475326
Cosine 142 = -0.788010753607
Tangent 142 = -0.781285626507
Cotangent 142 = -1.27994163219
Sine 143 = 0.601815023152
Cosine 143 = -0.798635510047
Tangent 143 = -0.753554050103
Cotangent 143 = -1.32704482162
Sine 144 = 0.587785252292
Cosine 144 = -0.809016994375
Tangent 144 = -0.726542528005
Cotangent 144 = -1.37638192047
Sine 145 = 0.573576436351
Cosine 145 = -0.819152044289
Tangent 145 = -0.70020753821
Cotangent 145 = -1.42814800674
Sine 146 = 0.559192903471
Cosine 146 = -0.829037572555
Tangent 146 = -0.674508516842
Cotangent 146 = -1.48256096851
Sine 147 = 0.544639035015
Cosine 147 = -0.838670567945
Tangent 147 = -0.649407593198
Cotangent 147 = -1.53986496381
Sine 148 = 0.529919264233
Cosine 148 = -0.848048096156
Tangent 148 = -0.624869351909
Cotangent 148 = -1.60033452904
Sine 149 = 0.51503807491
Cosine 149 = -0.857167300702
Tangent 149 = -0.600860619028
Cotangent 149 = -1.66427948235
Sine 150 = 0.5
Cosine 150 = -0.866025403784
Tangent 150 = -0.57735026919
Cotangent 150 = -1.73205080757
Sine 151 = 0.484809620246
Cosine 151 = -0.874619707139
Tangent 151 = -0.554309051453
Cotangent 151 = -1.80404775527
Sine 152 = 0.469471562786
Cosine 152 = -0.882947592859
Tangent 152 = -0.531709431661
Cotangent 152 = -1.88072646535
Sine 153 = 0.45399049974
Cosine 153 = -0.891006524188
Tangent 153 = -0.509525449494
Cotangent 153 = -1.96261050551
Sine 154 = 0.438371146789
Cosine 154 = -0.898794046299
Tangent 154 = -0.487732588566
Cotangent 154 = -2.05030384158
Sine 155 = 0.422618261741
Cosine 155 = -0.906307787037
Tangent 155 = -0.466307658155
Cotangent 155 = -2.14450692051
Sine 156 = 0.406736643076
Cosine 156 = -0.913545457643
Tangent 156 = -0.445228685309
Cotangent 156 = -2.2460367739
Sine 157 = 0.390731128489
Cosine 157 = -0.920504853452
Tangent 157 = -0.42447481621
Cotangent 157 = -2.35585236582
Sine 158 = 0.374606593416
Cosine 158 = -0.927183854567
Tangent 158 = -0.404026225835
Cotangent 158 = -2.47508685342
Sine 159 = 0.358367949545
Cosine 159 = -0.933580426497
Tangent 159 = -0.383864035035
Cotangent 159 = -2.60508906469
Sine 160 = 0.342020143326
Cosine 160 = -0.939692620786
Tangent 160 = -0.363970234266
Cotangent 160 = -2.74747741945
Sine 161 = 0.325568154457
Cosine 161 = -0.945518575599
Tangent 161 = -0.34432761329
Cotangent 161 = -2.90421087768
Sine 162 = 0.309016994375
Cosine 162 = -0.951056516295
Tangent 162 = -0.324919696233
Cotangent 162 = -3.07768353718
Sine 163 = 0.292371704723
Cosine 163 = -0.956304755963
Tangent 163 = -0.305730681459
Cotangent 163 = -3.27085261848
Sine 164 = 0.275637355817
Cosine 164 = -0.961261695938
Tangent 164 = -0.286745385759
Cotangent 164 = -3.48741444384
Sine 165 = 0.258819045103
Cosine 165 = -0.965925826289
Tangent 165 = -0.267949192431
Cotangent 165 = -3.73205080757
Sine 166 = 0.2419218956
Cosine 166 = -0.970295726276
Tangent 166 = -0.249328002843
Cotangent 166 = -4.01078093354
Sine 167 = 0.224951054344
Cosine 167 = -0.974370064785
Tangent 167 = -0.230868191126
Cotangent 167 = -4.33147587428
Sine 168 = 0.207911690818
Cosine 168 = -0.978147600734
Tangent 168 = -0.21255656167
Cotangent 168 = -4.70463010948
Sine 169 = 0.190808995377
Cosine 169 = -0.981627183448
Tangent 169 = -0.194380309138
Cotangent 169 = -5.14455401597
Sine 170 = 0.173648177667
Cosine 170 = -0.984807753012
Tangent 170 = -0.176326980708
Cotangent 170 = -5.67128181962
Sine 171 = 0.15643446504
Cosine 171 = -0.987688340595
Tangent 171 = -0.158384440325
Cotangent 171 = -6.31375151468
Sine 172 = 0.13917310096
Cosine 172 = -0.990268068742
Tangent 172 = -0.140540834702
Cotangent 172 = -7.11536972238
Sine 173 = 0.121869343405
Cosine 173 = -0.992546151641
Tangent 173 = -0.122784560903
Cotangent 173 = -8.14434642797
Sine 174 = 0.104528463268
Cosine 174 = -0.994521895368
Tangent 174 = -0.105104235266
Cotangent 174 = -9.51436445422
Sine 175 = 0.0871557427477
Cosine 175 = -0.996194698092
Tangent 175 = -0.0874886635259
Cotangent 175 = -11.4300523028
Sine 176 = 0.0697564737441
Cosine 176 = -0.99756405026
Tangent 176 = -0.0699268119435
Cotangent 176 = -14.3006662567
Sine 177 = 0.0523359562429
Cosine 177 = -0.998629534755
Tangent 177 = -0.052407779283
Cotangent 177 = -19.0811366877
Sine 178 = 0.0348994967025
Cosine 178 = -0.999390827019
Tangent 178 = -0.0349207694917
Cotangent 178 = -28.6362532829
Sine 179 = 0.0174524064373
Cosine 179 = -0.999847695156
Tangent 179 = -0.0174550649282
Cotangent 179 = -57.2899616308
Sine 180 = 0.0
Cosine 180 = -1.0
Tangent 180 = 0.0
Cotangent 180 = ∞
Sine 181 = -0.0174524064373
Cosinüs 181 = -0.999847695156
Tanjant 181 = 0.0174550649282
Cotanjant 181 = 57.2899616308
Sine 182 = -0.0348994967025
Cosinüs 182 = -0.999390827019
Tanjant 182 = 0.0349207694917
Cotanjant 182 = 28.6362532829
Sine 183 = -0.0523359562429
Cosinüs 183 = -0.998629534755
Tanjant 183 = 0.052407779283
Cotanjant 183 = 19.0811366877
Sine 184 = -0.0697564737441
Cosinüs 184 = -0.99756405026
Tanjant 184 = 0.0699268119435
Cotanjant 184 = 14.3006662567
Sine 185 = -0.0871557427477
Cosinüs 185 = -0.996194698092
Tanjant 185 = 0.0874886635259
Cotanjant 185 = 11.4300523028
Sine 186 = -0.104528463268
Cosinüs 186 = -0.994521895368
Tanjant 186 = 0.105104235266
Cotanjant 186 = 9.51436445422
Sine 187 = -0.121869343405
Cosinüs 187 = -0.992546151641
Tanjant 187 = 0.122784560903
Cotanjant 187 = 8.14434642797
Sine 188 = -0.13917310096
Cosinüs 188 = -0.990268068742
Tanjant 188 = 0.140540834702
Cotanjant 188 = 7.11536972238
Sine 189 = -0.15643446504
Cosinüs 189 = -0.987688340595
Tanjant 189 = 0.158384440325
Cotanjant 189 = 6.31375151468
Sine 190 = -0.173648177667
Cosinüs 190 = -0.984807753012
Tanjant 190 = 0.176326980708
Cotanjant 190 = 5.67128181962
Sine 191 = -0.190808995377
Cosinüs 191 = -0.981627183448
Tanjant 191 = 0.194380309138
Cotanjant 191 = 5.14455401597
Sine 192 = -0.207911690818
Cosinüs 192 = -0.978147600734
Tanjant 192 = 0.21255656167
Cotanjant 192 = 4.70463010948
Sine 193 = -0.224951054344
Cosinüs 193 = -0.974370064785
Tanjant 193 = 0.230868191126
Cotanjant 193 = 4.33147587428
Sine 194 = -0.2419218956
Cosinüs 194 = -0.970295726276
Tanjant 194 = 0.249328002843
Cotanjant 194 = 4.01078093354
Sine 195 = -0.258819045103
Cosinüs 195 = -0.965925826289
Tanjant 195 = 0.267949192431
Cotanjant 195 = 3.73205080757
Sine 196 = -0.275637355817
Cosinüs 196 = -0.961261695938
Tanjant 196 = 0.286745385759
Cotanjant 196 = 3.48741444384
Sine 197 = -0.292371704723
Cosinüs 197 = -0.956304755963
Tanjant 197 = 0.305730681459
Cotanjant 197 = 3.27085261848
Sine 198 = -0.309016994375
Cosinüs 198 = -0.951056516295
Tanjant 198 = 0.324919696233
Cotanjant 198 = 3.07768353718
Sine 199 = -0.325568154457
Cosinüs 199 = -0.945518575599
Tanjant 199 = 0.34432761329
Cotanjant 199 = 2.90421087768
Sine 200 = -0.342020143326
Cosinüs 200 = -0.939692620786
Tanjant 200 = 0.363970234266
Cotanjant 200 = 2.74747741945
Sine 201 = -0.358367949545
Cosinüs 201 = -0.933580426497
Tanjant 201 = 0.383864035035
Cotanjant 201 = 2.60508906469
Sine 202 = -0.374606593416
Cosinüs 202 = -0.927183854567
Tanjant 202 = 0.404026225835
Cotanjant 202 = 2.47508685342
Sine 203 = -0.390731128489
Cosinüs 203 = -0.920504853452
Tanjant 203 = 0.42447481621
Cotanjant 203 = 2.35585236582
Sine 204 = -0.406736643076
Cosinüs 204 = -0.913545457643
Tanjant 204 = 0.445228685309
Cotanjant 204 = 2.2460367739
Sine 205 = -0.422618261741
Cosinüs 205 = -0.906307787037
Tanjant 205 = 0.466307658155
Cotanjant 205 = 2.14450692051
Sine 206 = -0.438371146789
Cosinüs 206 = -0.898794046299
Tanjant 206 = 0.487732588566
Cotanjant 206 = 2.05030384158
Sine 207 = -0.45399049974
Cosinüs 207 = -0.891006524188
Tanjant 207 = 0.509525449494
Cotanjant 207 = 1.96261050551
Sine 208 = -0.469471562786
Cosinüs 208 = -0.882947592859
Tanjant 208 = 0.531709431661
Cotanjant 208 = 1.88072646535
Sine 209 = -0.484809620246
Cosinüs 209 = -0.874619707139
Tanjant 209 = 0.554309051453
Cotanjant 209 = 1.80404775527
Sine 210 = -0.5
Cosinüs 210 = -0.866025403784
Tanjant 210 = 0.57735026919
Cotanjant 210 = 1.73205080757
Sine 211 = -0.51503807491
Cosinüs 211 = -0.857167300702
Tanjant 211 = 0.600860619028
Cotanjant 211 = 1.66427948235
Sine 212 = -0.529919264233
Cosinüs 212 = -0.848048096156
Tanjant 212 = 0.624869351909
Cotanjant 212 = 1.60033452904
Sine 213 = -0.544639035015
Cosinüs 213 = -0.838670567945
Tanjant 213 = 0.649407593198
Cotanjant 213 = 1.53986496381
Sine 214 = -0.559192903471
Cosinüs 214 = -0.829037572555
Tanjant 214 = 0.674508516842
Cotanjant 214 = 1.48256096851
Sine 215 = -0.573576436351
Cosinüs 215 = -0.819152044289
Tanjant 215 = 0.70020753821
Cotanjant 215 = 1.42814800674
Sine 216 = -0.587785252292
Cosinüs 216 = -0.809016994375
Tanjant 216 = 0.726542528005
Cotanjant 216 = 1.37638192047
Sine 217 = -0.601815023152
Cosinüs 217 = -0.798635510047
Tanjant 217 = 0.753554050103
Cotanjant 217 = 1.32704482162
Sine 218 = -0.615661475326
Cosinüs 218 = -0.788010753607
Tanjant 218 = 0.781285626507
Cotanjant 218 = 1.27994163219
Sine 219 = -0.62932039105
Cosinüs 219 = -0.777145961457
Tanjant 219 = 0.809784033195
Cotanjant 219 = 1.23489715654
Sine 220 = -0.642787609687
Cosinüs 220 = -0.766044443119
Tanjant 220 = 0.839099631177
Cotanjant 220 = 1.19175359259
Sine 221 = -0.656059028991
Cosinüs 221 = -0.754709580223
Tanjant 221 = 0.869286737816
Cotanjant 221 = 1.15036840722
Sine 222 = -0.669130606359
Cosinüs 222 = -0.743144825477
Tanjant 222 = 0.900404044298
Cotanjant 222 = 1.11061251483
Sine 223 = -0.681998360062
Cosinüs 223 = -0.731353701619
Tanjant 223 = 0.932515086138
Cotanjant 223 = 1.07236871002
Sine 224 = -0.694658370459
Cosinüs 224 = -0.719339800339
Tanjant 224 = 0.965688774807
Cotanjant 224 = 1.03553031379
Sine 225 = -0.707106781187
Cosinüs 225 = -0.707106781187
Tanjant 225 = 1.0
Cotanjant 225 = 1.0
Sine 226 = -0.719339800339
Cosinüs 226 = -0.694658370459
Tanjant 226 = 1.03553031379
Cotanjant 226 = 0.965688774807
Sine 227 = -0.731353701619
Cosinüs 227 = -0.681998360062
Tanjant 227 = 1.07236871002
Cotanjant 227 = 0.932515086138
Sine 228 = -0.743144825477
Cosinüs 228 = -0.669130606359
Tanjant 228 = 1.11061251483
Cotanjant 228 = 0.900404044298
Sine 229 = -0.754709580223
Cosinüs 229 = -0.656059028991
Tanjant 229 = 1.15036840722
Cotanjant 229 = 0.869286737816
Sine 230 = -0.766044443119
Cosinüs 230 = -0.642787609687
Tanjant 230 = 1.19175359259
Cotanjant 230 = 0.839099631177
Sine 231 = -0.777145961457
Cosinüs 231 = -0.62932039105
Tanjant 231 = 1.23489715654
Cotanjant 231 = 0.809784033195
Sine 232 = -0.788010753607
Cosinüs 232 = -0.615661475326
Tanjant 232 = 1.27994163219
Cotanjant 232 = 0.781285626507
Sine 233 = -0.798635510047
Cosinüs 233 = -0.601815023152
Tanjant 233 = 1.32704482162
Cotanjant 233 = 0.753554050103
Sine 234 = -0.809016994375
Cosinüs 234 = -0.587785252292
Tanjant 234 = 1.37638192047
Cotanjant 234 = 0.726542528005
Sine 235 = -0.819152044289
Cosinüs 235 = -0.573576436351
Tanjant 235 = 1.42814800674
Cotanjant 235 = 0.70020753821
Sine 236 = -0.829037572555
Cosinüs 236 = -0.559192903471
Tanjant 236 = 1.48256096851
Cotanjant 236 = 0.674508516842
Sine 237 = -0.838670567945
Cosinüs 237 = -0.544639035015
Tanjant 237 = 1.53986496381
Cotanjant 237 = 0.649407593198
Sine 238 = -0.848048096156
Cosinüs 238 = -0.529919264233
Tanjant 238 = 1.60033452904
Cotanjant 238 = 0.624869351909
Sine 239 = -0.857167300702
Cosinüs 239 = -0.51503807491
Tanjant 239 = 1.66427948235
Cotanjant 239 = 0.600860619028
Sine 240 = -0.866025403784
Cosinüs 240 = -0.5
Tanjant 240 = 1.73205080757
Cotanjant 240 = 0.57735026919
Sine 241 = -0.874619707139
Cosinüs 241 = -0.484809620246
Tanjant 241 = 1.80404775527
Cotanjant 241 = 0.554309051453
Sine 242 = -0.882947592859
Cosinüs 242 = -0.469471562786
Tanjant 242 = 1.88072646535
Cotanjant 242 = 0.531709431661
Sine 243 = -0.891006524188
Cosinüs 243 = -0.45399049974
Tanjant 243 = 1.96261050551
Cotanjant 243 = 0.509525449494
Sine 244 = -0.898794046299
Cosinüs 244 = -0.438371146789
Tanjant 244 = 2.05030384158
Cotanjant 244 = 0.487732588566
Sine 245 = -0.906307787037
Cosinüs 245 = -0.422618261741
Tanjant 245 = 2.14450692051
Cotanjant 245 = 0.466307658155
Sine 246 = -0.913545457643
Cosinüs 246 = -0.406736643076
Tanjant 246 = 2.2460367739
Cotanjant 246 = 0.445228685309
Sine 247 = -0.920504853452
Cosinüs 247 = -0.390731128489
Tanjant 247 = 2.35585236582
Cotanjant 247 = 0.42447481621
Sine 248 = -0.927183854567
Cosinüs 248 = -0.374606593416
Tanjant 248 = 2.47508685342
Cotanjant 248 = 0.404026225835
Sine 249 = -0.933580426497
Cosinüs 249 = -0.358367949545
Tanjant 249 = 2.60508906469
Cotanjant 249 = 0.383864035035
Sine 250 = -0.939692620786
Cosinüs 250 = -0.342020143326
Tanjant 250 = 2.74747741945
Cotanjant 250 = 0.363970234266
Sine 251 = -0.945518575599
Cosinüs 251 = -0.325568154457
Tanjant 251 = 2.90421087768
Cotanjant 251 = 0.34432761329
Sine 252 = -0.951056516295
Cosinüs 252 = -0.309016994375
Tanjant 252 = 3.07768353718
Cotanjant 252 = 0.324919696233
Sine 253 = -0.956304755963
Cosinüs 253 = -0.292371704723
Tanjant 253 = 3.27085261848
Cotanjant 253 = 0.305730681459
Sine 254 = -0.961261695938
Cosinüs 254 = -0.275637355817
Tanjant 254 = 3.48741444384
Cotanjant 254 = 0.286745385759
Sine 255 = -0.965925826289
Cosinüs 255 = -0.258819045103
Tanjant 255 = 3.73205080757
Cotanjant 255 = 0.267949192431
Sine 256 = -0.970295726276
Cosinüs 256 = -0.2419218956
Tanjant 256 = 4.01078093354
Cotanjant 256 = 0.249328002843
Sine 257 = -0.974370064785
Cosinüs 257 = -0.224951054344
Tanjant 257 = 4.33147587428
Cotanjant 257 = 0.230868191126
Sine 258 = -0.978147600734
Cosinüs 258 = -0.207911690818
Tanjant 258 = 4.70463010948
Cotanjant 258 = 0.21255656167
Sine 259 = -0.981627183448
Cosinüs 259 = -0.190808995377
Tanjant 259 = 5.14455401597
Cotanjant 259 = 0.194380309138
Sine 260 = -0.984807753012
Cosinüs 260 = -0.173648177667
Tanjant 260 = 5.67128181962
Cotanjant 260 = 0.176326980708
Sine 261 = -0.987688340595
Cosinüs 261 = -0.15643446504
Tanjant 261 = 6.31375151468
Cotanjant 261 = 0.158384440325
Sine 262 = -0.990268068742
Cosinüs 262 = -0.13917310096
Tanjant 262 = 7.11536972238
Cotanjant 262 = 0.140540834702
Sine 263 = -0.992546151641
Cosinüs 263 = -0.121869343405
Tanjant 263 = 8.14434642797
Cotanjant 263 = 0.122784560903
Sine 264 = -0.994521895368
Cosinüs 264 = -0.104528463268
Tanjant 264 = 9.51436445422
Cotanjant 264 = 0.105104235266
Sine 265 = -0.996194698092
Cosinüs 265 = -0.0871557427477
Tanjant 265 = 11.4300523028
Cotanjant 265 = 0.0874886635259
Sine 266 = -0.99756405026
Cosinüs 266 = -0.0697564737441
Tanjant 266 = 14.3006662567
Cotanjant 266 = 0.0699268119435
Sine 267 = -0.998629534755
Cosinüs 267 = -0.0523359562429
Tanjant 267 = 19.0811366877
Cotanjant 267 = 0.052407779283
Sine 268 = -0.999390827019
Cosinüs 268 = -0.0348994967025
Tanjant 268 = 28.6362532829
Cotanjant 268 = 0.0349207694917
Sine 269 = -0.999847695156
Cosinüs 269 = -0.0174524064373
Tanjant 269 = 57.2899616308
Cotanjant 269 = 0.0174550649282
Sine 270 = -1.0
Cosinüs 270 = 0.0
Tanjant 270 = ∞
Cotanjant 270 = 0.0
Sine 271 = -0.999847695156
Cosinüs 271 = 0.0174524064373
Tanjant 271 = -57.2899616308
Cotanjant 271 = -0.0174550649282
Sine 272 = -0.999390827019
Cosinüs 272 = 0.0348994967025
Tanjant 272 = -28.6362532829
Cotanjant 272 = -0.0349207694917
Sine 273 = -0.998629534755
Cosinüs 273 = 0.0523359562429
Tanjant 273 = -19.0811366877
Cotanjant 273 = -0.052407779283
Sine 274 = -0.99756405026
Cosinüs 274 = 0.0697564737441
Tanjant 274 = -14.3006662567
Cotanjant 274 = -0.0699268119435
Sine 275 = -0.996194698092
Cosinüs 275 = 0.0871557427477
Tanjant 275 = -11.4300523028
Cotanjant 275 = -0.0874886635259
Sine 276 = -0.994521895368
Cosinüs 276 = 0.104528463268
Tanjant 276 = -9.51436445422
Cotanjant 276 = -0.105104235266
Sine 277 = -0.992546151641
Cosinüs 277 = 0.121869343405
Tanjant 277 = -8.14434642797
Cotanjant 277 = -0.122784560903
Sine 278 = -0.990268068742
Cosinüs 278 = 0.13917310096
Tanjant 278 = -7.11536972238
Cotanjant 278 = -0.140540834702
Sine 279 = -0.987688340595
Cosinüs 279 = 0.15643446504
Tanjant 279 = -6.31375151468
Cotanjant 279 = -0.158384440325
Sine 280 = -0.984807753012
Cosinüs 280 = 0.173648177667
Tanjant 280 = -5.67128181962
Cotanjant 280 = -0.176326980708
Sine 281 = -0.981627183448
Cosinüs 281 = 0.190808995377
Tanjant 281 = -5.14455401597
Cotanjant 281 = -0.194380309138
Sine 282 = -0.978147600734
Cosinüs 282 = 0.207911690818
Tanjant 282 = -4.70463010948
Cotanjant 282 = -0.21255656167
Sine 283 = -0.974370064785
Cosinüs 283 = 0.224951054344
Tanjant 283 = -4.33147587428
Cotanjant 283 = -0.230868191126
Sine 284 = -0.970295726276
Cosinüs 284 = 0.2419218956
Tanjant 284 = -4.01078093354
Cotanjant 284 = -0.249328002843
Sine 285 = -0.965925826289
Cosinüs 285 = 0.258819045103
Tanjant 285 = -3.73205080757
Cotanjant 285 = -0.267949192431
Sine 286 = -0.961261695938
Cosinüs 286 = 0.275637355817
Tanjant 286 = -3.48741444384
Cotanjant 286 = -0.286745385759
Sine 287 = -0.956304755963
Cosinüs 287 = 0.292371704723
Tanjant 287 = -3.27085261848
Cotanjant 287 = -0.305730681459
Sine 288 = -0.951056516295
Cosinüs 288 = 0.309016994375
Tanjant 288 = -3.07768353718
Cotanjant 288 = -0.324919696233
Sine 289 = -0.945518575599
Cosinüs 289 = 0.325568154457
Tanjant 289 = -2.90421087768
Cotanjant 289 = -0.34432761329
Sine 290 = -0.939692620786
Cosinüs 290 = 0.342020143326
Tanjant 290 = -2.74747741945
Cotanjant 290 = -0.363970234266
Sine 291 = -0.933580426497
Cosinüs 291 = 0.358367949545
Tanjant 291 = -2.60508906469
Cotanjant 291 = -0.383864035035
Sine 292 = -0.927183854567
Cosinüs 292 = 0.374606593416
Tanjant 292 = -2.47508685342
Cotanjant 292 = -0.404026225835
Sine 293 = -0.920504853452
Cosinüs 293 = 0.390731128489
Tanjant 293 = -2.35585236582
Cotanjant 293 = -0.42447481621
Sine 294 = -0.913545457643
Cosinüs 294 = 0.406736643076
Tanjant 294 = -2.2460367739
Cotanjant 294 = -0.445228685309
Sine 295 = -0.906307787037
Cosinüs 295 = 0.422618261741
Tanjant 295 = -2.14450692051
Cotanjant 295 = -0.466307658155
Sine 296 = -0.898794046299
Cosinüs 296 = 0.438371146789
Tanjant 296 = -2.05030384158
Cotanjant 296 = -0.487732588566
Sine 297 = -0.891006524188
Cosinüs 297 = 0.45399049974
Tanjant 297 = -1.96261050551
Cotanjant 297 = -0.509525449494
Sine 298 = -0.882947592859
Cosinüs 298 = 0.469471562786
Tanjant 298 = -1.88072646535
Cotanjant 298 = -0.531709431661
Sine 299 = -0.874619707139
Cosinüs 299 = 0.484809620246
Tanjant 299 = -1.80404775527
Cotanjant 299 = -0.554309051453
Sine 300 = -0.866025403784
Cosinüs 300 = 0.5
Tanjant 300 = -1.73205080757
Cotanjant 300 = -0.57735026919
Sine 301 = -0.857167300702
Cosinüs 301 = 0.51503807491
Tanjant 301 = -1.66427948235
Cotanjant 301 = -0.600860619028
Sine 302 = -0.848048096156
Cosinüs 302 = 0.529919264233
Tanjant 302 = -1.60033452904
Cotanjant 302 = -0.624869351909
Sine 303 = -0.838670567945
Cosinüs 303 = 0.544639035015
Tanjant 303 = -1.53986496381
Cotanjant 303 = -0.649407593198
Sine 304 = -0.829037572555
Cosinüs 304 = 0.559192903471
Tanjant 304 = -1.48256096851
Cotanjant 304 = -0.674508516842
Sine 305 = -0.819152044289
Cosinüs 305 = 0.573576436351
Tanjant 305 = -1.42814800674
Cotanjant 305 = -0.70020753821
Sine 306 = -0.809016994375
Cosinüs 306 = 0.587785252292
Tanjant 306 = -1.37638192047
Cotanjant 306 = -0.726542528005
Sine 307 = -0.798635510047
Cosinüs 307 = 0.601815023152
Tanjant 307 = -1.32704482162
Cotanjant 307 = -0.753554050103
Sine 308 = -0.788010753607
Cosinüs 308 = 0.615661475326
Tanjant 308 = -1.27994163219
Cotanjant 308 = -0.781285626507
Sine 309 = -0.777145961457
Cosinüs 309 = 0.62932039105
Tanjant 309 = -1.23489715654
Cotanjant 309 = -0.809784033195
Sine 310 = -0.766044443119
Cosinüs 310 = 0.642787609687
Tanjant 310 = -1.19175359259
Cotanjant 310 = -0.839099631177
Sine 311 = -0.754709580223
Cosinüs 311 = 0.656059028991
Tanjant 311 = -1.15036840722
Cotanjant 311 = -0.869286737816
Sine 312 = -0.743144825477
Cosinüs 312 = 0.669130606359
Tanjant 312 = -1.11061251483
Cotanjant 312 = -0.900404044298
Sine 313 = -0.731353701619
Cosinüs 313 = 0.681998360062
Tanjant 313 = -1.07236871002
Cotanjant 313 = -0.932515086138
Sine 314 = -0.719339800339
Cosinüs 314 = 0.694658370459
Tanjant 314 = -1.03553031379
Cotanjant 314 = -0.965688774807
Sine 315 = -0.707106781187
Cosinüs 315 = 0.707106781187
Tanjant 315 = -1.0
Cotanjant 315 = -1.0
Sine 316 = -0.694658370459
Cosinüs 316 = 0.719339800339
Tanjant 316 = -0.965688774807
Cotanjant 316 = -1.03553031379
Sine 317 = -0.681998360062
Cosinüs 317 = 0.731353701619
Tanjant 317 = -0.932515086138
Cotanjant 317 = -1.07236871002
Sine 318 = -0.669130606359
Cosinüs 318 = 0.743144825477
Tanjant 318 = -0.900404044298
Cotanjant 318 = -1.11061251483
Sine 319 = -0.656059028991
Cosinüs 319 = 0.754709580223
Tanjant 319 = -0.869286737816
Cotanjant 319 = -1.15036840722
Sine 320 = -0.642787609687
Cosinüs 320 = 0.766044443119
Tanjant 320 = -0.839099631177
Cotanjant 320 = -1.19175359259
Sine 321 = -0.62932039105
Cosinüs 321 = 0.777145961457
Tanjant 321 = -0.809784033195
Cotanjant 321 = -1.23489715654
Sine 322 = -0.615661475326
Cosinüs 322 = 0.788010753607
Tanjant 322 = -0.781285626507
Cotanjant 322 = -1.27994163219
Sine 323 = -0.601815023152
Cosinüs 323 = 0.798635510047
Tanjant 323 = -0.753554050103
Cotanjant 323 = -1.32704482162
Sine 324 = -0.587785252292
Cosinüs 324 = 0.809016994375
Tanjant 324 = -0.726542528005
Cotanjant 324 = -1.37638192047
Sine 325 = -0.573576436351
Cosinüs 325 = 0.819152044289
Tanjant 325 = -0.70020753821
Cotanjant 325 = -1.42814800674
Sine 326 = -0.559192903471
Cosinüs 326 = 0.829037572555
Tanjant 326 = -0.674508516842
Cotanjant 326 = -1.48256096851
Sine 327 = -0.544639035015
Cosinüs 327 = 0.838670567945
Tanjant 327 = -0.649407593198
Cotanjant 327 = -1.53986496381
Sine 328 = -0.529919264233
Cosinüs 328 = 0.848048096156
Tanjant 328 = -0.624869351909
Cotanjant 328 = -1.60033452904
Sine 329 = -0.51503807491
Cosinüs 329 = 0.857167300702
Tanjant 329 = -0.600860619028
Cotanjant 329 = -1.66427948235
Sine 330 = -0.5
Cosinüs 330 = 0.866025403784
Tanjant 330 = -0.57735026919
Cotanjant 330 = -1.73205080757
Sine 331 = -0.484809620246
Cosinüs 331 = 0.874619707139
Tanjant 331 = -0.554309051453
Cotanjant 331 = -1.80404775527
Sine 332 = -0.469471562786
Cosinüs 332 = 0.882947592859
Tanjant 332 = -0.531709431661
Cotanjant 332 = -1.88072646535
Sine 333 = -0.45399049974
Cosinüs 333 = 0.891006524188
Tanjant 333 = -0.509525449494
Cotanjant 333 = -1.96261050551
Sine 334 = -0.438371146789
Cosinüs 334 = 0.898794046299
Tanjant 334 = -0.487732588566
Cotanjant 334 = -2.05030384158
Sine 335 = -0.422618261741
Cosinüs 335 = 0.906307787037
Tanjant 335 = -0.466307658155
Cotanjant 335 = -2.14450692051
Sine 336 = -0.406736643076
Cosinüs 336 = 0.913545457643
Tanjant 336 = -0.445228685309
Cotanjant 336 = -2.2460367739
Sine 337 = -0.390731128489
Cosinüs 337 = 0.920504853452
Tanjant 337 = -0.42447481621
Cotanjant 337 = -2.35585236582
Sine 338 = -0.374606593416
Cosinüs 338 = 0.927183854567
Tanjant 338 = -0.404026225835
Cotanjant 338 = -2.47508685342
Sine 339 = -0.358367949545
Cosinüs 339 = 0.933580426497
Tanjant 339 = -0.383864035035
Cotanjant 339 = -2.60508906469
Sine 340 = -0.342020143326
Cosinüs 340 = 0.939692620786
Tanjant 340 = -0.363970234266
Cotanjant 340 = -2.74747741945
Sine 341 = -0.325568154457
Cosinüs 341 = 0.945518575599
Tanjant 341 = -0.34432761329
Cotanjant 341 = -2.90421087768
Sinüs 342 = -0.309016994375
Cosinüs 342 = 0.951056516295
Tanjant 342 = -0.324919696233
Cotanjant 342 = -3.07768353718
Sine 343 = -0.292371704723
Cosinüs 343 = 0.956304755963
Tanjant 343 = -0.305730681459
Cotanjant 343 = -3.27085261848
Sine 344 = -0.275637355817
Cosinüs 344 = 0.961261695938
Tanjant 344 = -0.286745385759
Cotanjant 344 = -3.48741444384
Sine 345 = -0.258819045103
Cosinüs 345 = 0.965925826289
Tanjant 345 = -0.267949192431
Cotanjant 345 = -3.73205080757
Sine 346 = -0.2419218956
Cosinüs 346 = 0.970295726276
Tanjant 346 = -0.249328002843
Cotanjant 346 = -4.01078093354
Sine 347 = -0.224951054344
Cosinüs 347 = 0.974370064785
Tanjant 347 = -0.230868191126
Cotanjant 347 = -4.33147587428
Sine 348 = -0.207911690818
Cosinüs 348 = 0.978147600734
Tanjant 348 = -0.21255656167
Cotanjant 348 = -4.70463010948
Sine 349 = -0.190808995377
Cosinüs 349 = 0.981627183448
Tanjant 349 = -0.194380309138
Cotanjant 349 = -5.14455401597
Sine 350 = -0.173648177667
Cosinüs 350 = 0.984807753012
Tanjant 350 = -0.176326980708
Cotanjant 350 = -5.67128181962
Sine 351 = -0.15643446504
Cosinüs 351 = 0.987688340595
Tanjant 351 = -0.158384440325
Cotanjant 351 = -6.31375151468
Sine 352 = -0.13917310096
Cosinüs 352 = 0.990268068742
Tanjant 352 = -0.140540834702
Cotanjant 352 = -7.11536972238
Sine 353 = -0.121869343405
Cosinüs 353 = 0.992546151641
Tanjant 353 = -0.122784560903
Cotanjant 353 = -8.14434642797
Sine 354 = -0.104528463268
Cosinüs 354 = 0.994521895368
Tanjant 354 = -0.105104235266
Cotanjant 354 = -9.51436445422
Sine 355 = -0.0871557427477
Cosinüs 355 = 0.996194698092
Tanjant 355 = -0.0874886635259
Cotanjant 355 = -11.4300523028
Sine 356 = -0.0697564737441
Cosinüs 356 = 0.99756405026
Tanjant 356 = -0.0699268119435
Cotanjant 356 = -14.3006662567
Sine 357 = -0.0523359562429
Cosinüs 357 = 0.998629534755
Tanjant 357 = -0.052407779283
Cotanjant 357 = -19.0811366877
Sine 358 = -0.03489949670 25
Cosinüs 358 = 0.999390827019
Tanjant 358 = -0.0349207694917
Cotanjant 358 = -28.6362532829
Sine 359 = -0.0174524064373
Cosinüs 359 = 0.999847695156
Tanjant 359 = -0.0174550649282
Cotanjant 359 = -57.2899616308
Sine 360 = 0.0
Cosinüs 360 = 1.0
Tanjant 360 = 0.0
Cotanjant 360 = ∞

To solve geometric problems;
-You must have basic knowledge of algebra.
-Don’t just look at the title text, but also carefully analyze the geometric shapes.
-Get to know the relevant geometric formulas sufficiently. It is very important to skillfully use the geometric formulas. If you are given an equilateral triangle, for example, then immediately envision the various formulas of the equilateral triangle.
-Use construction lines. If you can’t work on shape problems and have no idea, try to draw construction lines. Auxiliary lines are divided into construction lines inside graphics and expanded construction lines outside graphics. For many geometric shapes, many doubts about the problem will be resolved when the auxiliary lines are made correctly.
University exams the best thing you can do for math and geometry is practice so you can be sure that you can solve problems fast enough. The more you do something, the easier it is to go through the process of doing it. So, the more you practice on math geometry tests, the faster you will be solving problems.

Asya geometry book covers the most basic level geometry topics. “The most important claim that we are outside of traditional geometry teaching patterns is in the simplicity of our expression.”
All of the questions in the book have been solved, the questions have been solved in many ways and in detail, and the proofs of the necessary theorems have been made before the solution. The ability to comment on the solution was tried to be developed by establishing a link between the following questions. However; with its original design and solution technique, with a systematic question types from easy to difficult; It is aimed to increase the student’s study efficiency. I firmly believe that anyone who has sufficient or not enough knowledge of geometry, but who has an effort to learn, will benefit from this book.
(From Publicity Bulletin)


To study effectively, follow these techniques.
Every beginning is difficult. When friends start a business, the first resistance is the highest resistance in the process, and that resistance is constantly decreasing as the process continues. Therefore, although it may be difficult to start working at first, be sure that everything will work out and it will progress much easier.
Get out of your comfort zone.

If you want to work efficiently, you should definitely remove the distracting factors such as messaging, social media, web browsing, TV.
Put restrictions on your phone. Turn off all notifications. Incoming whatsApp notification, new photo from Instagram, even the news you read there can change your whole mood. Instagram, facebook, sms, calls, whatever, turn off everything that can make a sound or vibrate the phone.
Take a break from the TV, don’t panic, nothing escapes. When the time comes, you will be able to watch them all over the internet again and again.
Keep your desk tidy.

The simpler your desk is, the more relaxed your brain will be. Having only the courses you will study in your field of study will make it much easier for you to focus. So please don’t be lazy and try to keep your table tidy as much as you can. Remove unnecessary items.
Do not eat heavy meals before class.
When the stomach is full, the blood of the body increases. It renders the mind inoperable. Understanding disappears. It enters into laziness and laziness. It will be difficult to continue studying. If a person eats a lot, he drinks a lot of water, and a person who drinks a lot sleeps a lot. For this reason, it prevents you from taking sleep away and therefore from your productive study. In addition, diseases accumulate in the body. Because the main cause of diseases is eating too much and mixing of excess substances in the stomach.
Set your own learning time.
Everyone’s learning style is different. Do you like to work day or night? As it is learned better in the early hours of the day, evening can be the most productive time for learning. So first get to know yourself.
Get your sleep well.

After the scientific researches, it was seen that sleeping was more memorable than what was learned. Those who get up at night and work from sunrise to noon, take a nap, store information in the best way. You say that I don’t remember how I should do it.
Learn by teaching.

To improve memory and recall skills when we learn new information become a teacher teach that subject to someone. Explain everything you understand as if you were teaching someone a lesson.
With scientific research, it has been determined that the information stays in the mind more when the lesson is taught as if you are teaching it to someone. Namely, people remember what they read 10%, hear 20%, see 30%, both see and hear 50%, argue with someone 70%, personal experiences 80%, and what they teach others 95%.
Explain the subject you are trying to learn over and over again as if you are the teacher and someone else is in front of you. Say it a little louder.
Take notes.

One of the most productive working methods is to work by typing. Working with typing keeps more information in your mind.
According to a study conducted between a group of students who took notes and a group of students who just listened, questions were asked about the topic, and when you look at both groups, when you compare them, it is seen that most of them remember the same thing in the short term, but students who take notes stay in their minds more in the long term.
For example, what are we studying in geometry lesson today, are we studying trigonometry? I take notes of what the teacher tells and writes about trigonometry. On the one hand, I summarize and take notes of important formulas. On the one hand, my brain begins to memorize both what I hear and what I see. Because when I write, I see on the one hand and I practice on the other hand. Writing is very valuable in this sense.
So if you don’t want to forget what you learned at school, make sure to take notes.
If you study at home, learn to take notes. This can be a little tricky because it takes time. Writing is a bit of a chore, your hands may get tired and so on… But if you ask what is the most efficient study technique, note-taking is underlined.
Write the important headlines in red, the ones that may appear in the exam in green, and the warnings in blue because the colored texts will attract attention. You should review your notes and concepts that you read in class at least once a week, if not every day.
Practice memorization.
After reading a topic, close your books and remove your notes. Practice long-term memorization by saying out loud everything you can remember about that topic.
Use time by dividing it. (Pomodoro Method)

As you know the Pomodoro method, you give a 5-minute break after 25 minutes of working time. You loop these times and repeat. Rest yourself during the 5-minute break and continue to study the subject again with your head rested.
When you start working, the thought that I must do what I need to do as soon as possible will give you a great motivation
If the 25 minutes study time is too short, you can adjust it according to the topic you need to study or the test time you need to solve. First you start with 25 minutes, then you can progress by increasing it to 40 minutes, 50 minutes. In the end, you should care about the subject you need to finish, not the breaks..
Do exercises to relax.
Have a calm mind.

Unfortunately, we feed on so many negative things that the movies, news and programs we watch make us think negatively. The less you are exposed to them, the better.
Remove negative thoughts from your mind, try to attract positive thoughts to your mind. For every sentence you use negatively, use the positive instead of every word. Do not allow negative thoughts in your life. Follow it like a watchman.
Stay away from people who spread negative and negative energy. When you’re with those people, you turn negative. Complaining, finding fault, etc. Everything that has such a negative structure both takes your energy and causes you to turn from positive to negative. That’s why you should stay away from them.

Geometry is a branch of mathematics that deals with the study of spatial relationships, shapes, and sizes. It is concerned with the properties and measurements of points, lines, angles, surfaces, and solids in space. The word “geometry” comes from the Greek words “geo” meaning “earth” and “metron” meaning “measure”, which reflects the original focus of the subject on the measurement of distances, areas, and volumes in the physical world.
Geometry has many practical applications in fields such as architecture, engineering, physics, and computer graphics. It is also an important part of the secondary school mathematics curriculum, where students learn about concepts such as points, lines, angles, polygons, circles, and three-dimensional shapes, as well as how to use geometry to solve problems and prove mathematical theorems. Geometry plays a crucial role in helping us understand the structure of the world around us and in providing a foundation for further study in mathematics and science.
Even though geometry is a subject area originated from the mathematics studies, it is undoubtedly one of the most fundamental areas of research serving to solve everyday problems of humanity and explain the way our world works.
Thus, we can find geometry in every corner of our lives. In fact, the rise of geometry starts with philosophers and thinkers observing the nature and things around them. One of the most fascinating and deep-rooted practices of the world. If you think that geometry is just a challenging topic at school you might want to dive into its rich history.
This elegant practice originates from the concerns of everyday life and has a long past starting from 3100 BCE in Egypt and Mesopotamia.
Here are some specific examples of how geometry is used in different areas:
Architecture: Architects use geometry to design and create building plans, ensuring that structures are safe and functional. They also use geometry to calculate areas, volumes, and dimensions of spaces and objects.
Engineering: Engineers use geometry to design and build everything from bridges and tunnels to airplanes and spacecraft. They use geometric principles to ensure that these structures are safe and stable.
Computer Graphics: Computer graphics use geometry to create realistic 3D models of objects and environments. This is used in various industries such as video game design, film special effects, and virtual reality simulations.
Physics: Geometry is used in physics to understand the shape and structure of objects in space. For example, the principles of geometry are used to study the shapes of planets, stars, and galaxies.
Surveying: Surveyors use geometry to measure and map land and other physical features. They use geometric principles to calculate distances, angles, and areas of land.
These are just a few examples of how geometry is used in various fields. In general, geometry is used to understand the world around us and to solve problems related to shapes and spaces.
A few old societies there fostered a type of geometry fit to the connections between lengths, regions, and volumes of actual items. This geometry was systematized in Euclid’s Elements around 300 BCE based on 10 aphorisms, or hypotheses, from which a few hundred hypotheses were demonstrated by rational rationale. The Elements exemplified the proverbial logical technique for a long time.
Scientific geometry was started by the French mathematician René Descartes (1596-1650), who acquainted rectangular directions with finding focuses and empowering lines and bends to be addressed with logarithmic conditions. Logarithmic geometry is a cutting-edge expansion of the subject to multi-faceted and non-Euclidean spaces.
Projective geometry started with the French mathematician Girard Desargues (1591-1661) to manage those properties of mathematical figures that are not changed by projecting their picture, or “shadow,” onto another surface.
The German mathematician Carl Friedrich Gauss (1777-1855), regarding useful issues of looking over and geodesy, started the field of differential geometry. Utilizing differential analytics, he described the inborn properties of bends and surfaces. For example, he showed that the natural ebb and flow of a chamber is equivalent to that of a plane, as should be visible to cutting a chamber along its hub and straightening, however not equivalent to that of a circle, which can’t be smoothed without contortion.
Starting in the nineteenth 100 years, different mathematicians subbed options in contrast to Euclid’s equal proposal, which, in its cutting edge structure, peruses, “given a line and a point not on the line, it is feasible to define precisely one boundary through the given guide lined up toward the line.” They would have liked to show that the choices were sensibly unthinkable. All things considered, they found that steady non-Euclidean calculations exist.
The works of European geometers are known as modern geometry. Some of the most important figures of modern geometry are Descartes, Gauss, Newton, Riemann, and Leibniz. Geometers of the modern age have dealt with non-euclidian geometry. Analytic geometry which uses algebra to represent and solve problems in geometry was first initiated by the French mathematician Rene Descartes in hopes to understand the non-Euclidian spaces.
Another important product of modern geometry is the development of differential geometry which deals with properties of curves and surfaces using differential calculus.
Ultimately, geometry is an elegant practice standing upon a philosophical foundation, shining a light upon the day-to-day problems, and helping us understand the mysterious ways of the World.
The greatest minds of the time planted the origins of geometry to try and solve the problems with land sharing, building, and measuring storage areas. But geometry, as we know it today, has risen in the 6th century BCE and owes its evolution to the great Greek philosophers such as Aristotle, Plato, and many others. Greek philosophers are also the ones to coin the word “geometry” which is essentially the combination of the Greek words geo (“Earth”) and metron (“measure”).
Geometry has found solid ground with the influence of Greek logic and philosophy. Starting from Thales, Greek philosophers have created different ways of thinking that have act as the basis for geometry.

Thales of Miletus is the first person known to practice scientific philosophy. He used geometry to calculate the height of the Egyptian Pyramids and long distances. Thales is also the first person to be attributed a mathematical discovery with the Thales’ Theorem.

Pythagoras was a Greek mathematician. The date and place of his birth are both unknown. He seems to have been born between 580 and 568 BC. He leave his stamp on geometry and mathematics. Considered as one of the most important Greek philosophers, he influenced many other philosophers such as Plato and latemathematicians. Pythagoras has left behind the Pythagorean theorem and the theory of proportions which are the cornerstone of geometry even in the 21st century.
Various stories are told of his parantage, but it was believed that his father was Mnesarchus, a merchant from Tyre and his mother Pythais a native of Samos. He is often described as the first pure mathematician who has contributed immensely towards the development of mathematics. However, we know relatively little about his mathematical achievements. We have nothing much of Pythagoras writings and he remains a mysterious figure.
Little is known about his early life. As a child Pythagoras spent his early years in Samos but travelled widely with his father. Certainly he was well educated, learning to play the lyre, learning poetry and to recite Homer, Three philosophers influenced him when he was a young man. They were Pherekydes, Thales and his pupil Anaximander. He visited Egyptian on the advice of his teacher Thales in order to study the “earth measurement” of Egyptian priests. Later he became more popular than his master. He used to deliver lectures on philosophy and mathematics. His lectures were heard by persons of all ranks.
The influence of Pythagoras on his listeners was so great that they formed themselves into a society called ‘order of Pythagoreaus’. This influence was more religious than political. Theano, the daughter of his host, was the most attentive listener. Pythagoras later married Theano, who wrote a biography of her husband, which is not traceable.
Pythagoras never embodied his findings in any treatise. Due to the lack of good writing material he followed the custom of his time in passing his philosophy along by words of mouth. In the absence of written documents it becomes difficult to separate the work of Pythagoras himself from what is available at present in the form of Pythagorean contributions.

Plato, who is known as the “maker of mathematicians” has not only contributed to the rise of geometry but also educated numerous valuable geometers and mathematicians.
He is known for the identification of 5 regular symmetrical 3-dimensional shapes, which he considered as the basis for the whole universe. These geometric shapes known as platonic solids are tetrahedron, octahedron, icosahedron, cube, and dodecahedron. For Plato, each of these shapes represents different elements such as fire, air, water, and earth while the dodecahedron represents the harmony of constellations.
At Plato’s door, “Non-geometricians cannot enter our house!” the inscription is transmitted.

We can’t talk about geometry without mentioning Archimedes. He is regarded as one of the greatest scientists of all time and the oldest mathematician. Considered as one of the most popular mathematics in mathematics and physics, Archimedes has contributed a great deal to the evolution of geometry.
Archimedes produced much mathematical and geometric work. He has spent most of his young life solving arithmetic problems, including building techniques to calculate volume and surface space, defining pi, and building compound arithmetic. He not only knew the price of water and other things, but he also invented things.
His favorite activity was a mathematical model consisting of a globe with a cylinder of wide width. Archimedes has shown that the surface area is four times larger than that of the circle and that the volume of the sector is two-thirds the volume of the surrounding cylinder and the surface two-thirds of the surface of the surrounding cylinder, including its bases.
Archimedes was a scientist who completed his pioneer career in hydrostatic geometry. In geometry, he went on to work on Book XII of the Euclidean Elements. The problems he addressed and his solutions were at an all-time high.
Several Eastern thinkers followed and criticized the work of Euclid and contributed to the new areas of geometry. Euclid, Abul Wafa al-Buzjani, Omar Khayyam, Nasir al-Din al-Tusi and many others showed great works on geometry.

Euclid (300 BC) has the distinction of being the only man to summarise all the mathematical knowledge of his times. Beyond the fact that he taught at Alexandria, we know nothing with certainly about Euclid himself. It is possible that he may have been an Egyptian and not a Greek. He systematised Greek mathematics that was existed at the time. It is certain that Euclid taught mathematics about 300 BC in the Royal School at Alexandria in Egypt that had been founded by king Ptolemy the successor of Alexander, the great. His own education was probably acquired in Plato’s academy at Athens. He learnt the geometry of Eudoxus and Thealtetus of which he was familiar.
His book elements, the world’s most authoritative text on Geometry has made Euclid the father of Geometry. This mathematic treatise has been the centre of mathematics for 200 years. This has been used for centuries in Western Europe as Geometry Textbook. Alongwith ‘Element’ he wrote several books during his teaching profession for about 30 years. Once Ptolemy asked Euclid if there were any shorter way to study Geometry than throught the 13 books of the Elements, and Euclid replied that there was no royal road to geometry. The book ‘Elements’ is the greatest text book of all times. It was translated to various languages.
In this work, Euclid created a series of definitions of basic objects like points, straight lines, parallel lines surfaces, angles, circles and triangles, andaxioms. The Euclidean geometry we know today is based on these definitions and postulated derived from them. This is why Euclid’s influence on geometry is indisputable. His ‘Elements’ began with construction problems and the reader learned that a figure could be drawn Euclid collected all the geometrical facts known in his days, arranged the various theorems in proper order, improved their proofs where necessary and added theorems he himself had thought out.
He presented earlier mathematician’s work in a single, logically coherent framework, making it easy to use and reference in a beautiful way in elements. Euclid followed the steps of Aristotle in scientific philosophy and affected the world of mathematics and geometry irrefutably.
The year and the reason behind Euclid’s death is unknown to mankind. However, there have been vague appropriations that suggest that he might have perished around 260 BC. His books and treatises were sold and used by personalities all over the world until the 19th Century. It is said that Lincoln would religiously carry the ‘Elements’ with him wherever he would go, and would often quote the genius of Euclid’s work in his speeches. Even after Euclid’s death, Mathematician continued to write theorems and his work under his name.

Abul Wafa al-Buzjani was a Persian mathematician and astronomer who lived in the 10th century. He made important contributions to the fields of geometry and trigonometry.
Working on understanding the Moon’s orbit, he wrote “theories of the Moon” which included valuable information such as the first introduction of the tangent, secant,and cosecant functions and improvement in calculations for trigonometrical tables. For his valuable contributions, a crater on the Moon is named after Abul Wafa. His work on spherical triangles is also one of his most important contributions to geometry.
He also worked on the classification of quadrilaterals and developed a formula for finding the area of any quadrilateral given the lengths of its sides and one of its diagonals. He was also interested in the geometry of conic sections, including the parabola and ellipse.
In addition to his work in pure geometry, Abul Wafa applied his geometric knowledge to solve problems in astronomy and surveying. He developed a method for determining the direction of Mecca from any location using only a sundial and simple geometric constructions. He also worked on the problem of finding the direction of Qibla (the direction of prayer) for Muslims.
Abul Wafa’s work in geometry and trigonometry was highly influential, and his ideas were transmitted to later generations of mathematicians in both the Islamic world and Europe. His theorems and formulas continue to be studied and used in modern mathematics today, demonstrating his lasting impact on the field.

Omar Khayyam is one of the most influential Islamic mathematicians. He was a Persian polymath who lived in the 11th and 12th centuries. He was born in Nishapur, Iran, in 1048 and died in 1131. Khayyam was a scholar in multiple fields, including mathematics, geometry, astronomy, philosophy, and poetry
Omar Khayyam made significant contributions to the field of geometry during his lifetime. He is well-known for constructing the quadrilateral with two equal sides perpendicular to the base. He developed a new method for constructing a regular heptagon (a seven-sided polygon with equal sides and angles) using only a compass and straightedge. His work on the geometrical method of solving cubic equations by intersecting a parabola with a circle has created great attention.
Furthermore, Khayyam contributed to the study of Euclidean geometry, making several important discoveries and proofs. He discovered some non-Euclidian properties while looking to prove Euclid’s fifth postulate. Although he did not succeed in his attempt, his work on the subject influenced later mathematicians and contributed to the development of non-Euclidean geometries.
Overall, Omar Khayyam’s work in geometry was innovative and influential, and it contributed significantly to the development of modern mathematics. His insights and discoveries continue to be studied and admired by mathematicians today.
Question 144-) ABCD is trapezoidal, | DB | = 20 cm, if m (CBD) = 15 °; how many cm² is the area of the trapezoid?
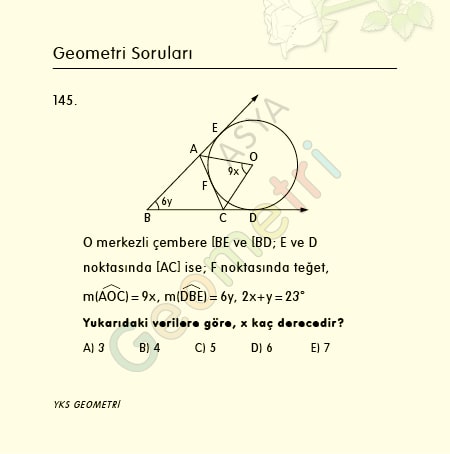
Question 145-) O centered circle [BE and [BD; [AC] at point E and D; Tangent to point F, m (AOC) = 9x, m (DBE) = 6y, 2x + 3y = 23 °, how many degrees is x?

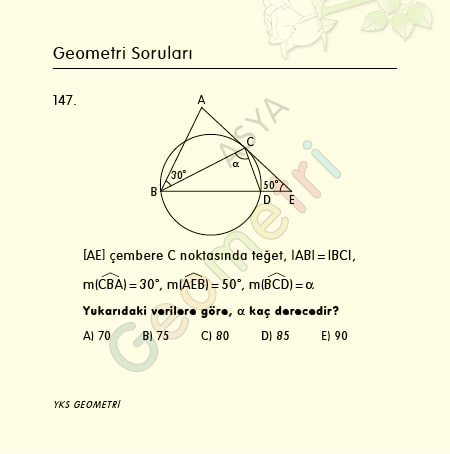
Question 146-) [ND]; Tangent to the circle centered B at point F, perpendicular to [NK] [BD], | NK | = | BC | = | CD | if; How many degrees is m (DBN)?
Question 147-) If [AE] is tangent to the circle at point C, | AB | = | BC |, m (CBA) = 30 °, m (AEB) = 50 °, m (BCD) = α; How many degrees is α?

Question 148-) If the center of the semicircle is | AE | = | ED | = | DC |, the size of the arc CB is 36 °, m (BAE) = x; How many degrees is x?

Question 149-) In the circle in the figure, if m (ACB) = 25 °, m (CBA) = 75 °, m (DBE) = α; How many degrees is α?
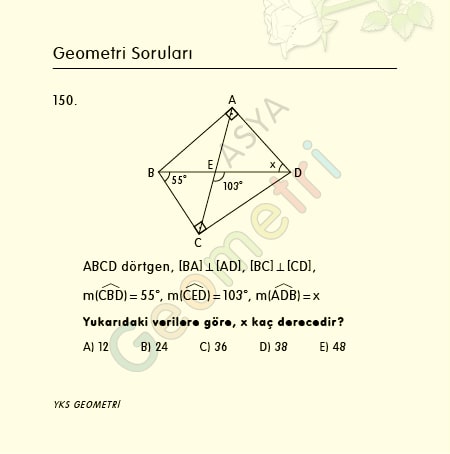
Question 150-) ABCD quadrilateral, perpendicular to [BA] [AD], perpendicular to [BC] [CD], if m (CBD) = 55 °, m (CED) = 103 °; How many degrees is m (ADB) = x?
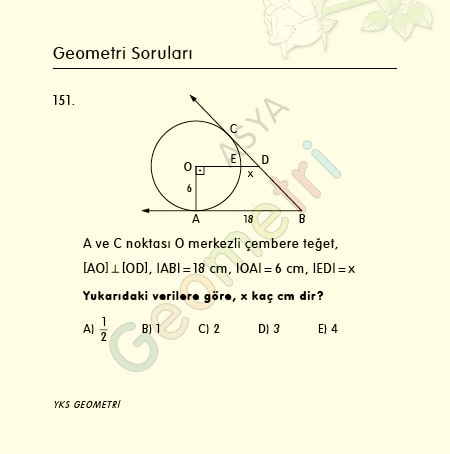
Question 151-) If points A and C are tangent to the circle centered O, perpendicular to [AO] [OD], | AB | = 18 cm, | OA | = 6 cm; | ED | = How many degrees is x?

Question 152-) The C corner of the CDOE square in the figure is on the O-centered circle arc, and the D and E corners are on the [AP] beam. Accordingly, how many degrees is m (POA)?

Question 153-) If ABCD is a square, B centered quarter circle, [DC] diameter semicircle, A, E and F are linear, m (FED) = α; How many degrees is α?
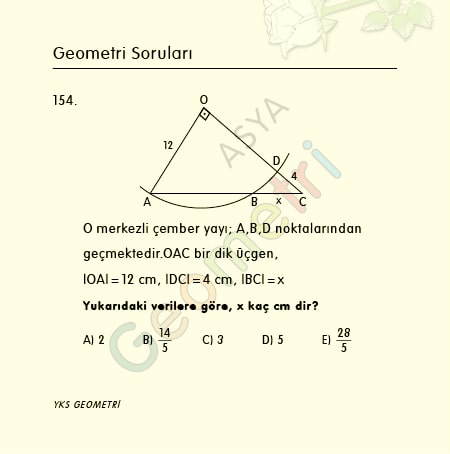
Question 154-) O-centered circle arc; It passes through the points A, B, D. OAC is a right triangle, | OA | = 12 cm, | DC | = 4 cm, | BC | = x; How many cm is x?
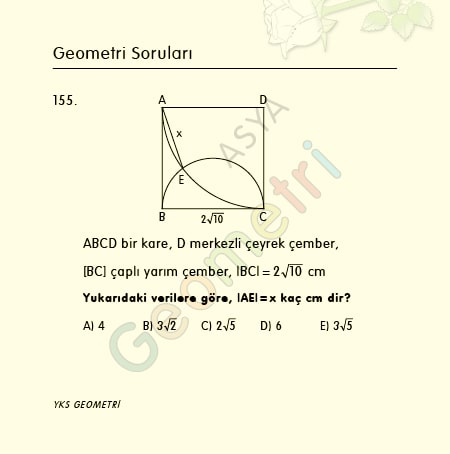
Question 155-) If ABCD is a square, D centered quarter circle, [BC] diameter semicircle, | BC | = 2 root 10 cm; | AE | = how many cm is x?

Question 156-) If the centered semicircle is ABOD and OFEC is the contour | FP | = 4 cm, | EF | = 8 cm; What is cm2’s of the hatched area?

Question 131-) In the figure, ABCD is rectangular, parallel to [BE] [CF], if 2 | AE | = 3 | EF |, | BE | = 3 root2 cm, | CF | = 13 root2 cm, m (BCF) = 45 °; What is the area of the rectangle?

Question 132-) ABCD square, S; If the cut-off point of [AC] and [EF] is | BF | = 3 cm, | ED | = 6 cm, | AB | = 18 cm; How many cm² is the area of the SFC triangle?
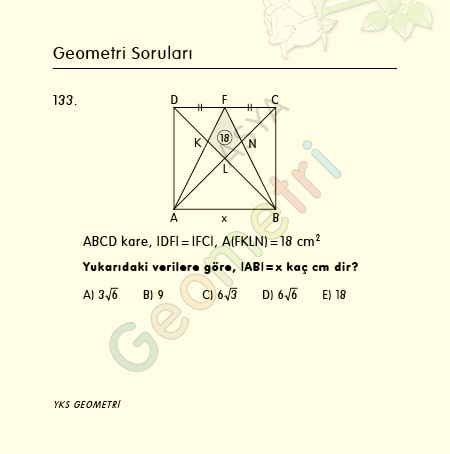
Question 133-) If the area of ABCD square, | DF | = | FC |, FKLN convex quadrilateral is 18 cm²; What is the length of a square in centimeters?
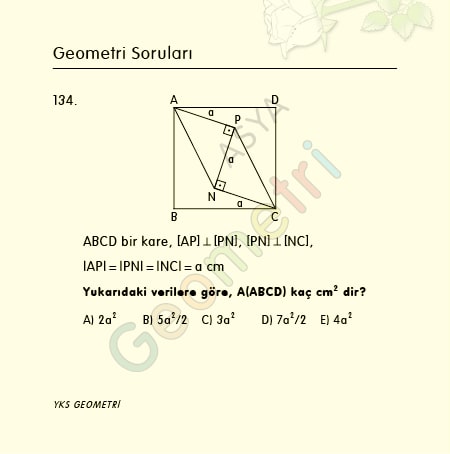
Question 134-) ABCD square, perpendicular to [AP] [PN], perpendicular to [PN] [NC], | AP | = | PN | = | NC | if; What is the area of the square in cm²?

Question 135-) If ABCD is rectangle, [AC] diagonal, perpendicular to [SN] [ND], | AB | = | NC |, | AS | = 1 cm, | SD | = 8 cm; | AN | = how many cm is x?
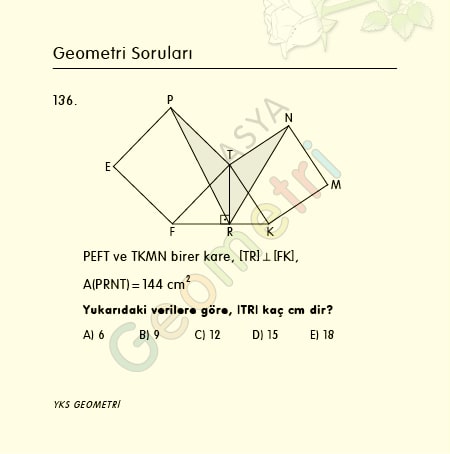
Question 136-) If PEFT and TKMN are square, perpendicular to [TR] [FK], PRNT concave quadrilateral is 144 cm²; | TR | how many cm?
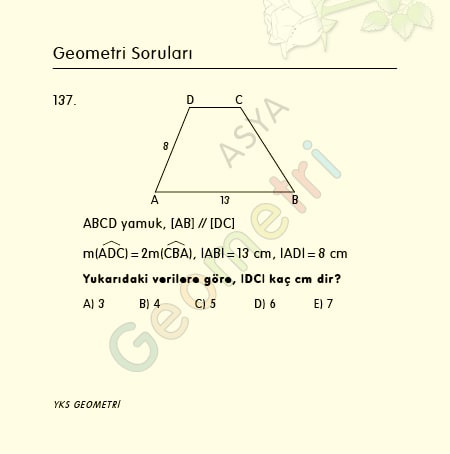
Question 137-) ABCD is trapezoid, [AB] parallel [DC], if the measure of angle D is twice the measure of angle B, the length of the bottom base is 13 cm, the length of [AD] is 8 cm; What is the length of the upper sole?
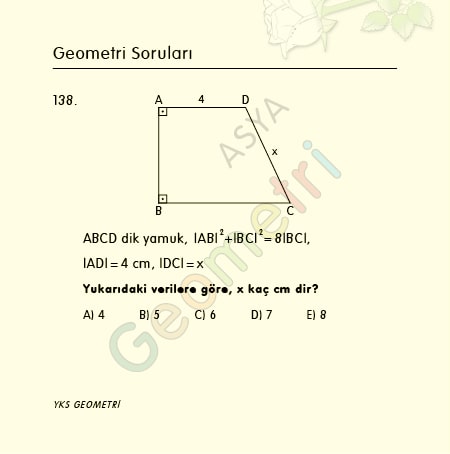
Question 138-) ABCD steep trapezoid, | AB | ² + | BC | ² = 8 | BC | if the length of the upper base is 4 cm; how many cm is the side x?
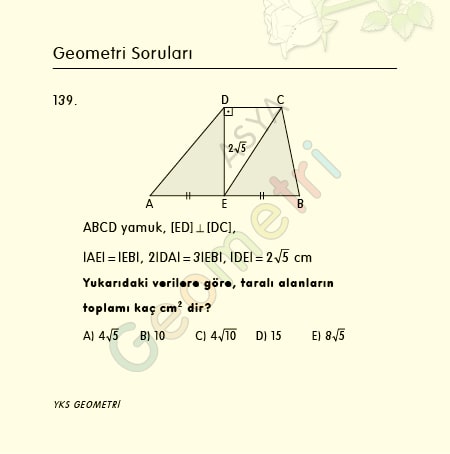
Question 139-) ABCD is trapezoid, [ED] perpendicular [DC], point E is the midpoint of the subbase, 2 | DA | = 3 | EB |, if the height is 2 root 5 cm; What is the total of shaded areas in cm²?
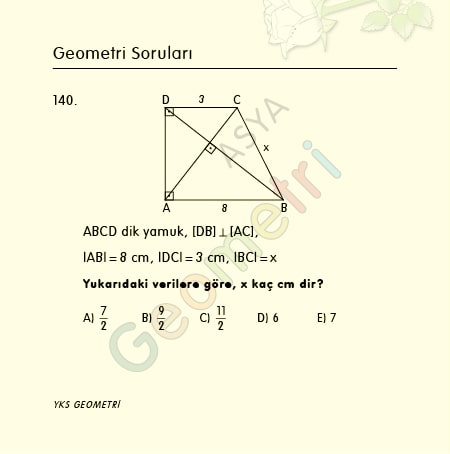
Question 140-) If the diagonals of the trapezoid ABCD are perpendicular to each other, the length of the upper base is 3 cm, the length of the lower base is 8 cm; how many cm is the side x?
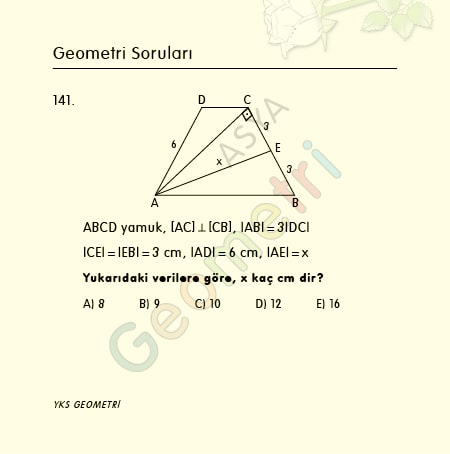
Question 141-) ABCD isosceles trapezoid, CAB right triangle, lower base 3 times the upper base, | AD | = 6 cm, | CE | = | EB | if; | AE | = how many cm is x?
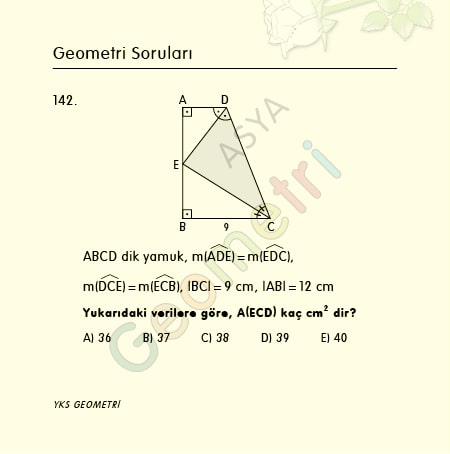
Question 142-) If ABCD is trapezoid perpendicular, [DE] and [CE] bisector, | BC | = 9 cm, | AB | = 12 cm; What is the area of the ECD triangle?
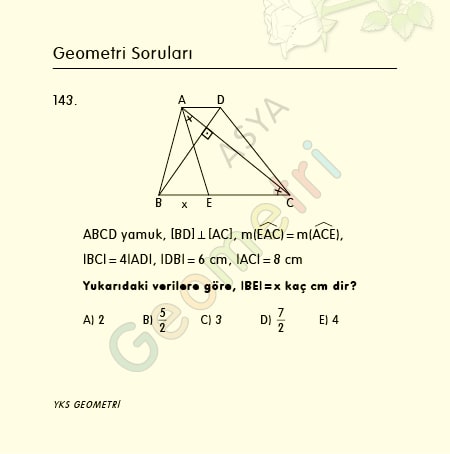
Question 143-) ABCD is trapezoid perpendicular, diagonals 6 cm-8 cm and perpendicular to each other, m (EAC) = m (AEC), if the lower floor is 4 times the upper floor; | BE | = how many cm is x?
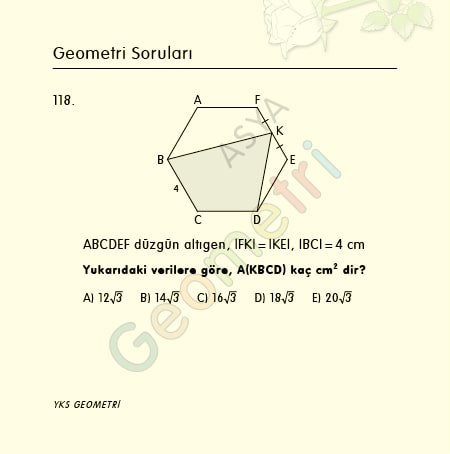
Question 118-) If ABCDEF is a regular hexagon, | FK | = | KE |, | BC | = 4 cm; What is the area of quadrilateral KBCD?
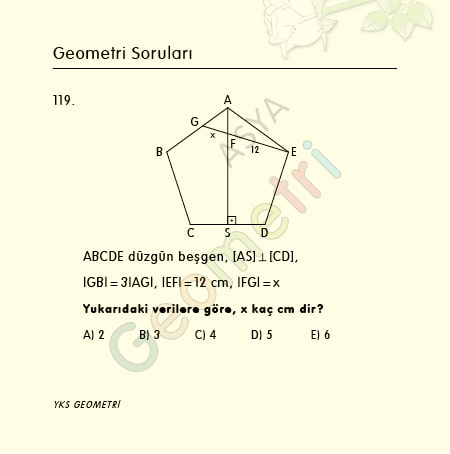
Question 119-) If ABCDE is regular pentagon, [AS] symmetry axis, | GB | = 3 | AG |, | EF | = 12 cm; | FG | = how many cm is x?
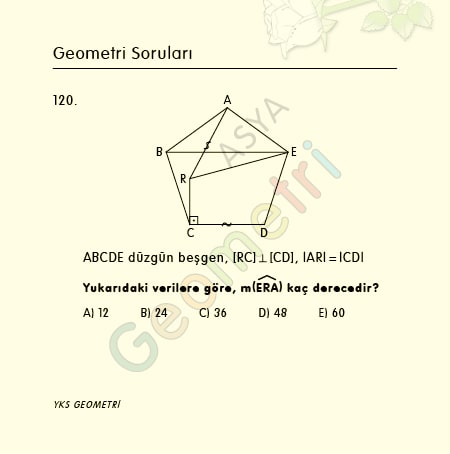
Question 120-) ABCDE is regular pentagon, [RC] perpendicular [CD], | AR | = | CD | if; What is the measure of the ERA angle?
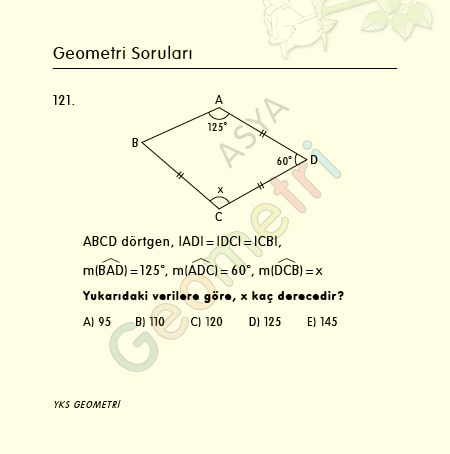
Question 121-) Quadrilateral ABCD, | AD | = | DC | = | CB |, if the measure of angle A is 125 ° and the measure of angle D is 60 °; The measure of angle C = how many degrees is x?
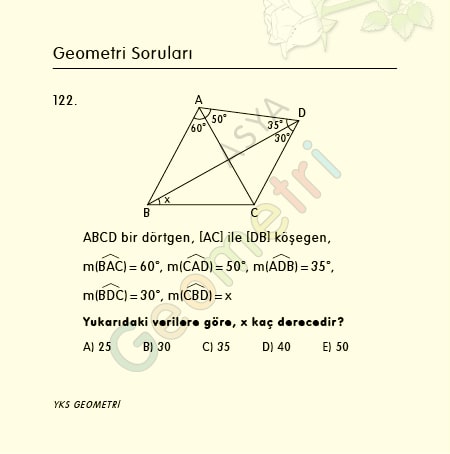
Question 122-) ABCD quadrilateral, if [AC] and [DB] diagonal, m (BAC) = 60 °, m (CAD) = 50 °, m (ADB) = 35 °, m (BDC) = 30 °; How many degrees is m (CBD) = x?
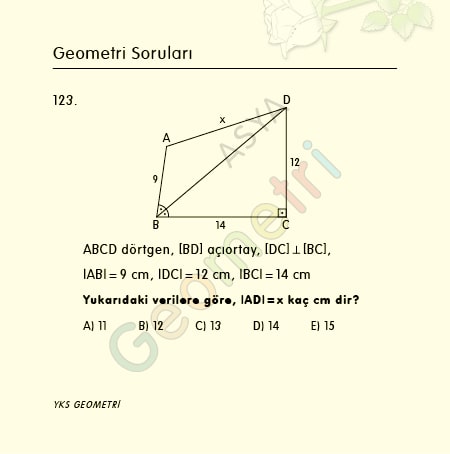
Question 123-) ABCD quadrilateral, [BD] bisector, [DC]; Perpendicular to [BC], if | AB | = 9 cm, | DC | = 12 cm, | BC | = 14 cm; | AD | = how many cm is x?
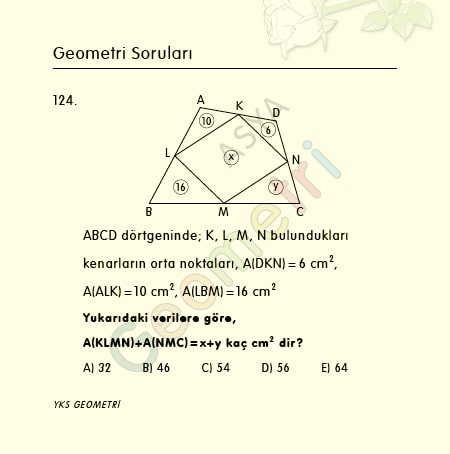
Question 124-) In quadrilateral ABCD; The midpoints of the edges where K, L, M, N are located, If Area (DKN) = 6 cm², Area (ALK) = 10 cm², Area (LBM) = 16 cm²; Area (KLMN) + Area (NMC) = x + y how many cm²?
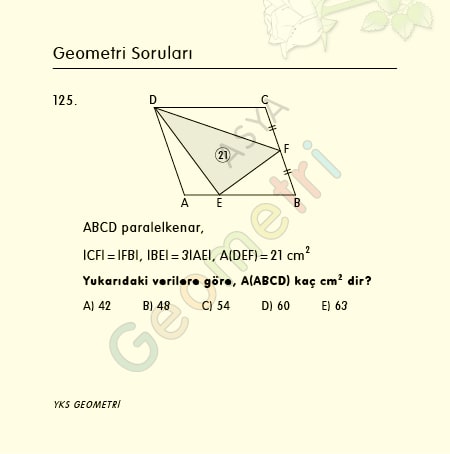
Question 125-) ABCD parallelogram, | CF | = | FB |, | BE | = 3 | AE |, If area (DEF) = 21 cm²; How many cm² is the area of the parallelogram?
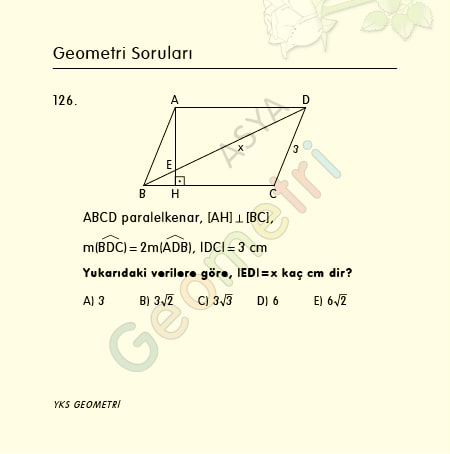
Question 126-) ABCD parallelogram, [AH]; Perpendicular to [BC], if m (BDC) = 2m (ADB), | DC | = 3 cm; | ED | = how many cm is x?
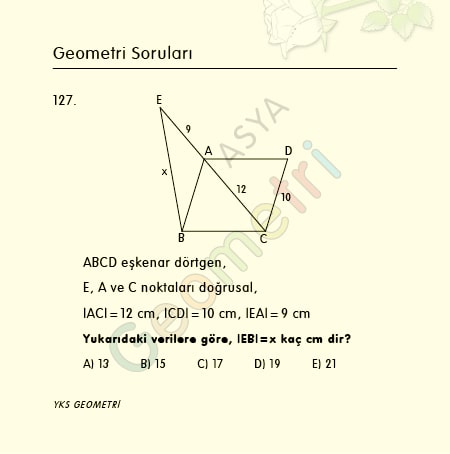
Question 127-) If ABCD is rhombus, points E, A and C are linear, | AC | = 12 cm, | CD | = 10 cm, | EA | = 9 cm; | EB | = how many cm is x?
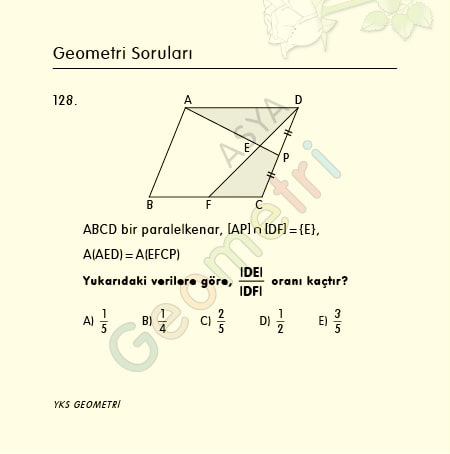
Question 128-) ABCD parallelogram, if the points A, E, P and D, E, F are linear, Area (AED) = Area (EFCP); | DE | / | DF | What is the rate?
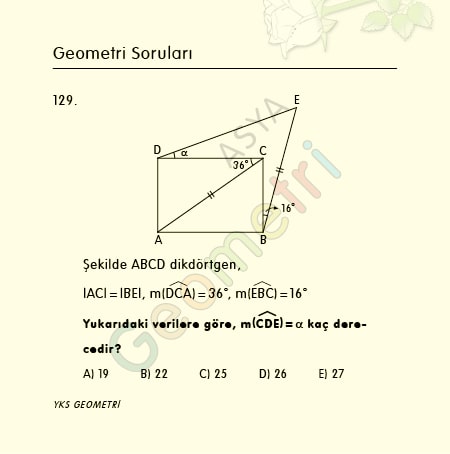
Question 129-) In the figure ABCD is a rectangle, if | AC | = | BE |, m (DCA) = 36 °, m (EBC) = 16 °; How many degrees is m (CDE) = α?
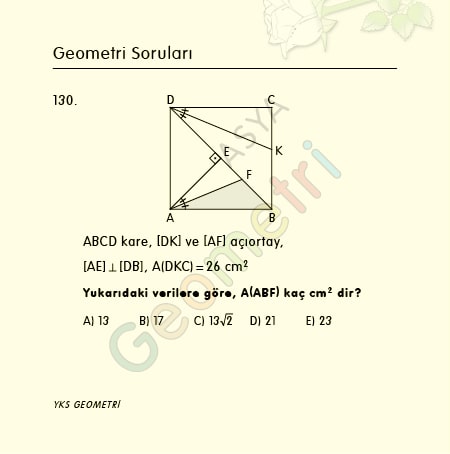
Question 130-) If ABCD square, [DK] and [AF] bisector, perpendicular to [AE] [DB], if the area of the DKC triangle is 26 cm²; What is the area of triangle ABF in cm²?
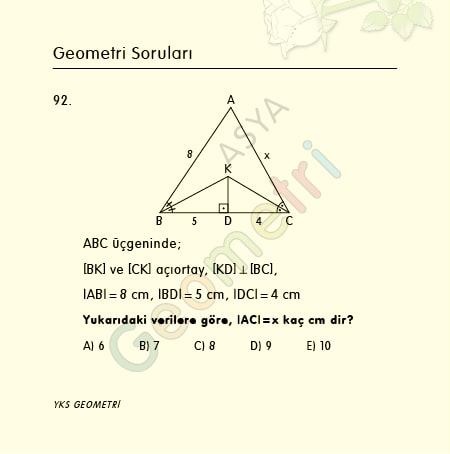
Question 92-) In triangle ABC, if [BK] and [CK] bisector, [KD] perpendicular [BC], | AB | = 8 cm, | BD | = 7 cm, | DC | = 4 cm; | AC | = how many cm is x?
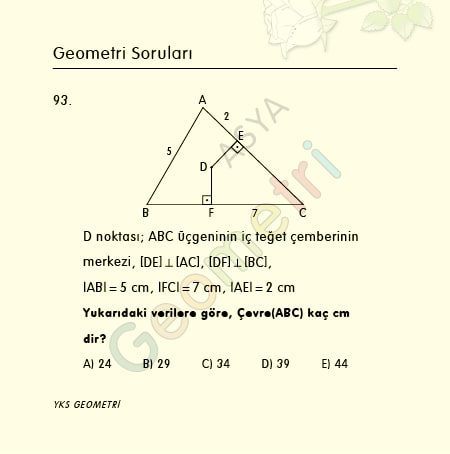
Question 93-) If point D is the center of the inner tangent circle of triangle ABC, [DE] perpendicular [AC], [DF] perpendicular [BC], | AB | = 5 cm, | FC | = 7 cm, | AE | = 2 cm ; How many cm is the circumference (ABC)?
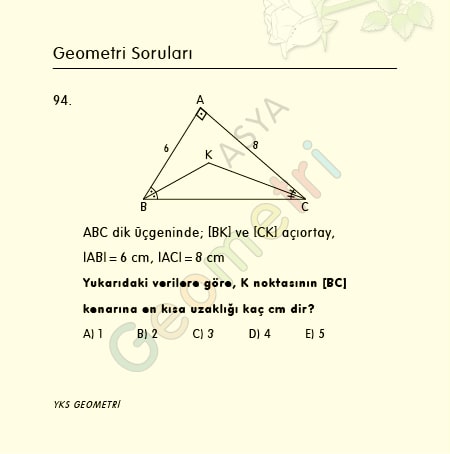
Question 94-) In the right triangle ABC, if [BK] and [CK] are bisector, | AB | = 6 cm, | AC | = 8 cm; What is the shortest distance of point K from the edge of [BC] in centimeters?

Question 95-) In the KBC triangle [BK] if perpendicular [KN], m (CBP) = m (PBK), | KN | = | NC |, | KF | = 3 cm, | BF | = 9 cm; | KP | = How many cm is x?
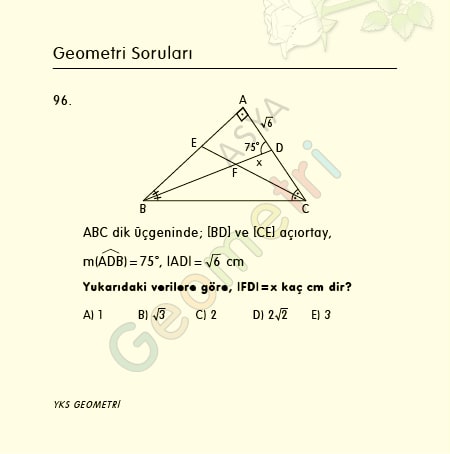
Question 96-) In the right triangle ABC, if [BD] and [CE] bisector, m (ADB) = 75 °, | AD | = root 6 cm; | FD | = how many cm is x?
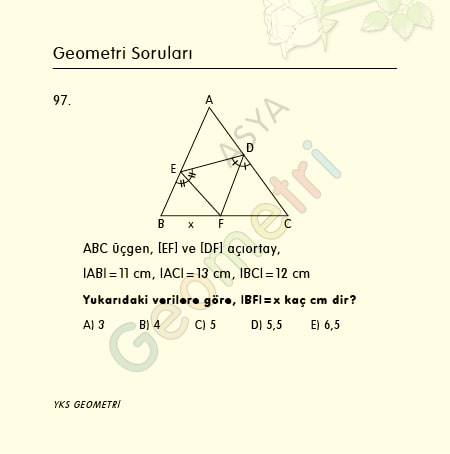
Question 97-) If ABC triangle, [EF] and [DF] bisector, | AB | = 11 cm, | AC | = 13 cm, | BC | = 12 cm; | BF | = how many cm is x?
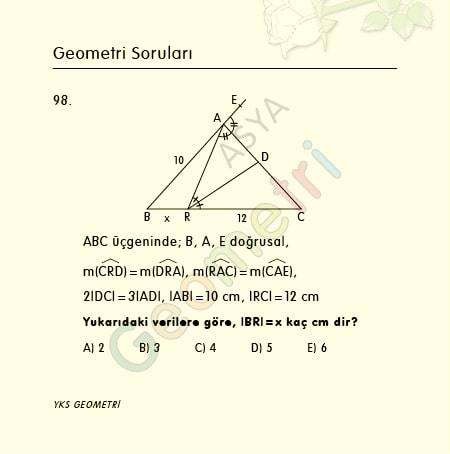
Question 98-) B, A, E linear in ABC triangle, m (CRD) = m (DRA), m (RAC) = m (CAE), 2 | DC | = 3 | AD |, | AB | = 10 cm, If | RC | = 12 cm; | BR | = how many cm is x?
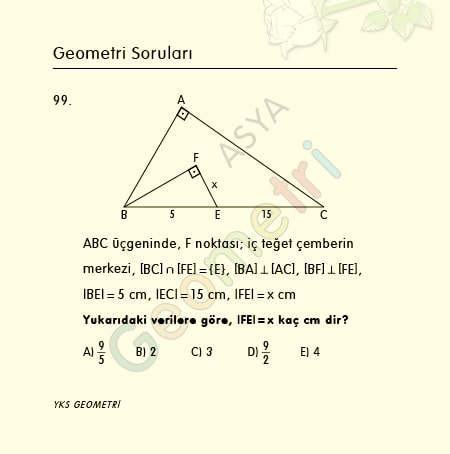
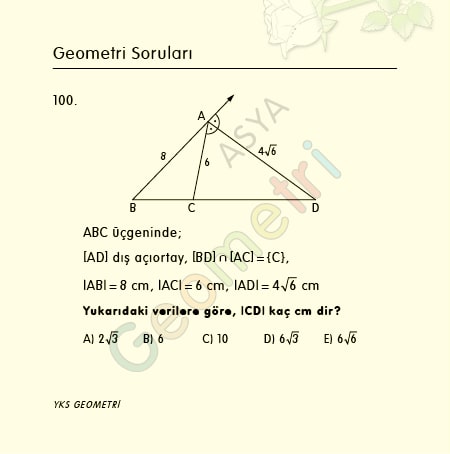
Question 100-) In triangle ABC [AD] outer bisector, if [BD] ∩ [AC] = {C}, | AB | = 8 cm, | AC | = 6 cm, | AD | = 4k root6 cm; | CD | how many cm?
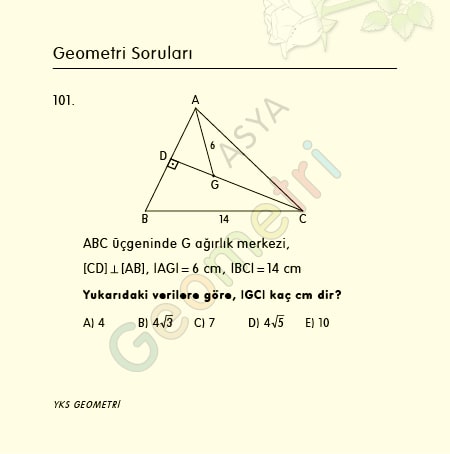
Question 101-) The center of gravity G in triangle ABC, [CD]; Perpendicular to [AB], if | AG | = 6 cm, | BC | = 14 cm; | GC | how many cm?

Question 102-) If the center of gravity G in ABC triangle is | GR | = | RB |, | GF | = 4 cm; | AG | how many cm?
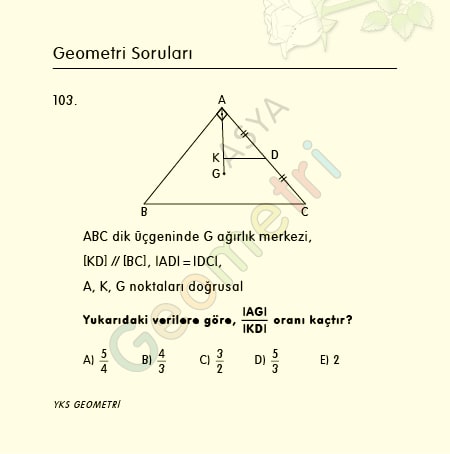
Question 103-) The center of gravity G in the right triangle ABC, [KD]; Parallel to [BC], if the points A, K, G are linear; | AG | / | KD | What is the rate?

Question 104-) The center of gravity G in the right triangle ABC, [AG]; Perpendicular to [GB], [DE]; Perpendicular to [BC], | AD | = | DG | if; How many degrees is m (GBA) = α?
One of thex greatest advantages of working with a geometry tutor is ddthe opportunity for individualized instruction. The tutor can...
What is 45 45 90 Triangle (Isosceles Right Triangle)? The 45-45-90 triangle gets its name from two equal angles and...
The 30-60-90 triangle is a special right triangle widely used in trigonometry because it has well-defined relationships between its angles...
The most important thing to study geometry is to be enthusiastic and to deal with it from your heart. Geometry...
The trigonometric table contains the calculated values of the trigonometric functions for a given angle from 0 to 360 degrees....
To solve geometric problems; -You must have basic knowledge of algebra. -Don’t just look at the title text, but also...
Asya geometry book covers the most basic level geometry topics. “The most important claim that we are outside of traditional...
To study effectively, follow these techniques. Every beginning is difficult. When friends start a business, the first resistance is the...
What is Geometry in Math? Geometry is a branch of mathematics that deals with the study of spatial relationships, shapes,...