Angles of a Triangle Test-1

Angles of a triangle test-1 …
Angles of a Triangle Test-1
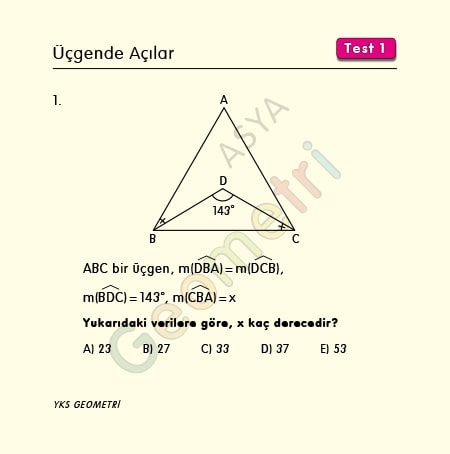
Problem 1 :
In triangle ABC, if ∠DBA equals ∠DCB and ∠BDC measures 143°, what is the measure of ∠CBA?
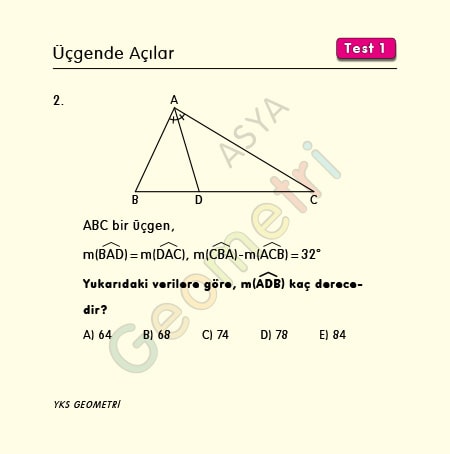
Problem 2 :
If ABC is a triangle, m (BAD) = m (DAC), m (CBA) – m (ACB) = 32 °; How many degrees is m (ADB)?
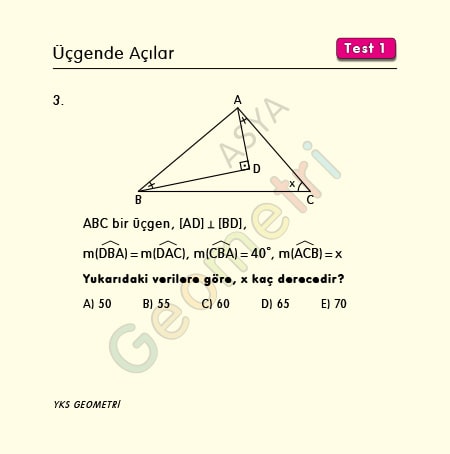
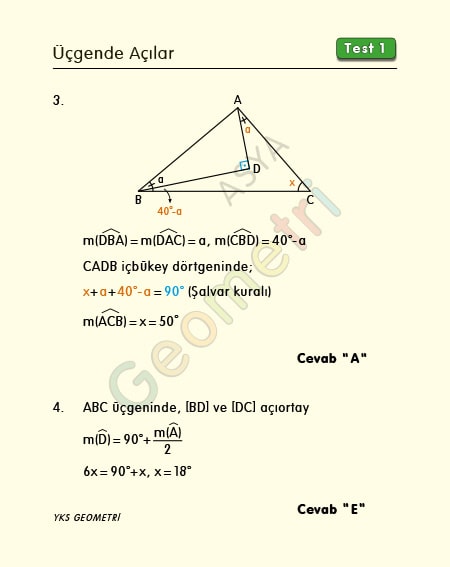
Problem 3 :
If ABC is a triangle, [AD] perpendicular [BD], m (DBA) = m (DAC), m (CBA) = 40 °; How many degrees is m (ACB) = x?
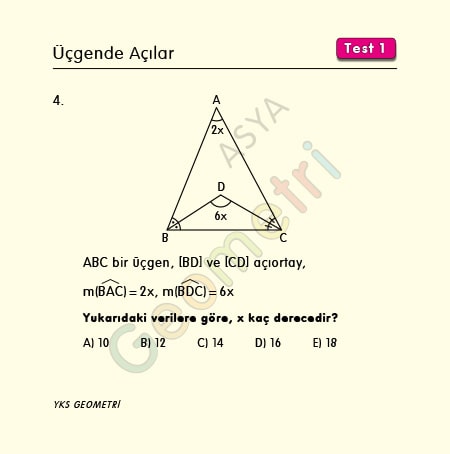
Problem 4 :
If ABC is a triangle, [BD] and [CD] bisector, m (BAC) = 2x, m (BDC) = 6x; How many degrees is x?
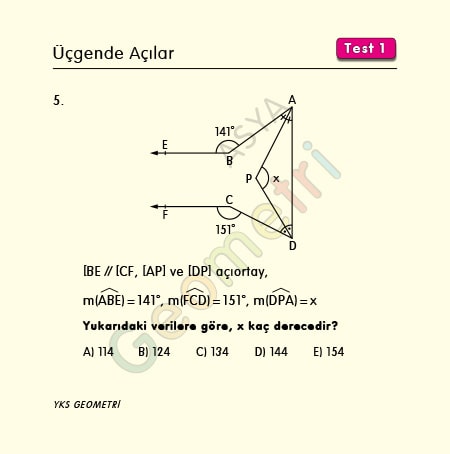
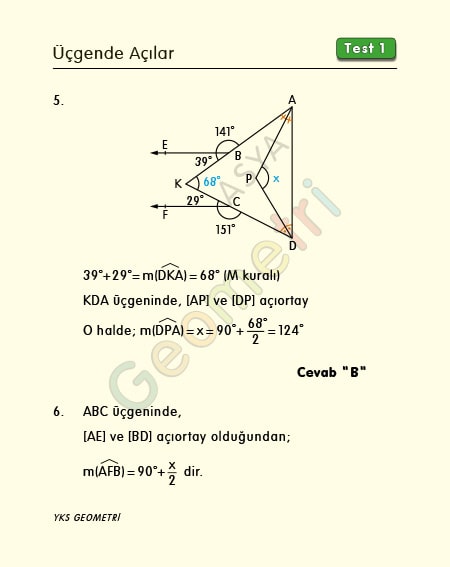
Problem 5 :
[BE parallel [CF, [AP] and [DP] bisector, if m (ABE) = 141 °, m (FCD) = 151 °; How many degrees is m (DPA) = x?
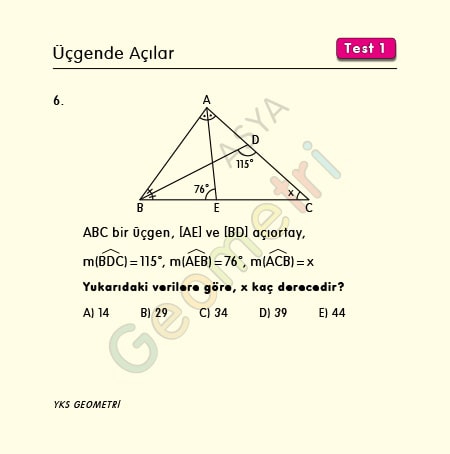
Problem 6 :
If ABC is a triangle, [AE] and [BD] bisector, m (BDC) = 115 °, m (AEB) = 76 °; How many degrees is m (ACB) = x?
Problem 7 :
If ABC is a triangle, [BD] and [CD] bisector, m (EAF) = 14x, m (CDB) = 11x; How many degrees is x?

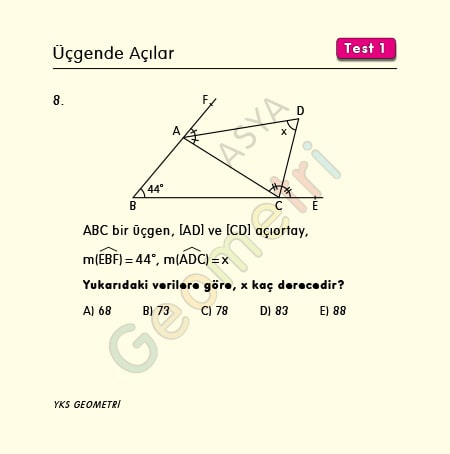
Problem 8 :
ABC is a triangle, [BD] and [CD] bisector, if m (EBF) = 44 °; How many degrees is m (ADC) = x?
Angles of a Triangle Test-1 Solutions
Solution of Problem 1 :
Triangle Angles and Evaluation
It is a fundamental rule that the sum of interior angles in a triangle always equals 180°. Let’s examine the given information with this principle in mind:
Assume that both angles ∠DBA and ∠DCB are denoted by the variable (a).
The measure of angle CBD is (x – a). This arises from the fact that ∠CBA is equal to (x).
Since the total of interior angles in triangle △DBC is always 180°:
(143 + (x – a) + a = 180°)
By solving the above equation::
(x = 37°)
Consequently, the value of (x) is determined to be 37°.
Solution of Problem 2 :
From the sum of the angles of the US triangle, x + n = 180 ° -m (ADB), in the ADC triangle from the outer angle y + n = m (ADB). Multiply the second expression by (-2) and add xy = 180 to the side by the first. ° -2m (ADB). If 32 ° is written instead of x, m (ADB) = 74 °.

Solution of Problem 3 :
The size of the angle formed when one side of the triangle is bent inward is x = a + b + c. The US concave quadrilateral contains x + a + 40 ° -a = 90 ° (shalwar, rocket, missile rule), x = 50 °. See geometry proofs section for proof of rule-Rocket rule-Missile rule and other proofs.
Solution of Problem 4 :
The size of the angle formed by the two inner bisectors in a triangle is 90 degrees more than half the size of the inside angle in the third corner, so 6x = 90 ° + x, x = 18 °.
Solution of Problem 5 :
Let the extension [AB] and [DC] intersect at point K. With the rule of M, m (DKA) = 68 °. The dimension of the angle formed by the intersection of two bisector in the triangle AKD is x = 90 ° + (68 ° / 2) = 124 ° .
Solution of Problem 6 :
Since [AE] and [BD] are bisectors in triangle ABC, m (AFB) = 90 ° + (x / 2). If the angles of the quadrant equal 360 °, then x = 34 °.
Solution of Problem 7 :
The measure of the angle formed by the two outer bisectors in a triangle is the complement of half the measure of the angle in the third corner. 11x = 90 ° – (14x / 2), x = 5 °.
Solution of Problem 8 :
The angle between the two outer bisectors is x = 90 ° – (44 ° / 2) = 68 °.


Angles of a Triangle test-1 PDF
Course Geometry offers Geometry textbook in pdf format that can be downloaded free of charge. Students can view the angles of a triangle test-1 pdf, which is important for university entrance exam, which aims to improve students’ problem solving skills.