Special Right Triangles Test-1

Special right triangles test-1 … 30 60 90 triangle, 45 45 90 triangle, 15 75 90 triangle, 15 30 135 triangle, euclidean, pythagorus, magnificent triangles, special triangle questions according to sides and angles.
Special Right Triangles Test-1 Problems
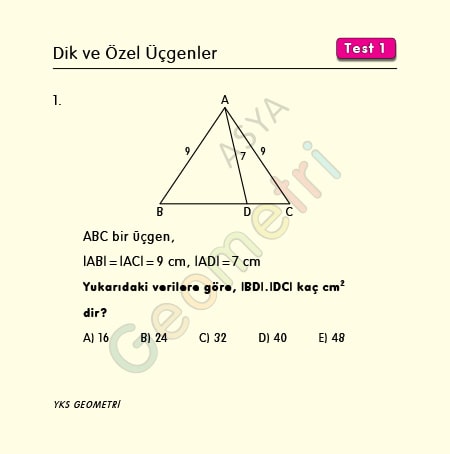
Problem 1 :
If ABC is a triangle, | AB | = | AC | = 9 cm, | AD | = 7 cm; | BD |. | DC | how many cm²?
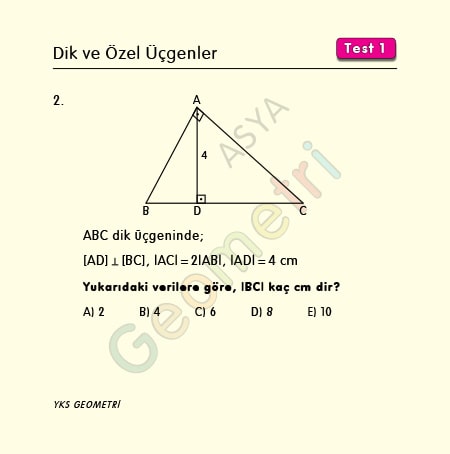
Problem 2 :
In right triangle ABC, if [AD] perpendicular [BC], | AC | = 2 | AB |, | AD | = 4 cm; what is the length of BC?
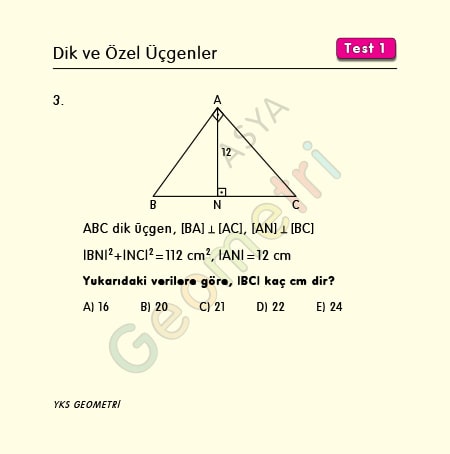
Problem 3 :
If ABC right triangle, [BA] perpendicular [AC], [AN] perpendicular [BC], | BN | ² + | NC | ² = 112 cm², | AN | = 12 cm; what is the length of BC?
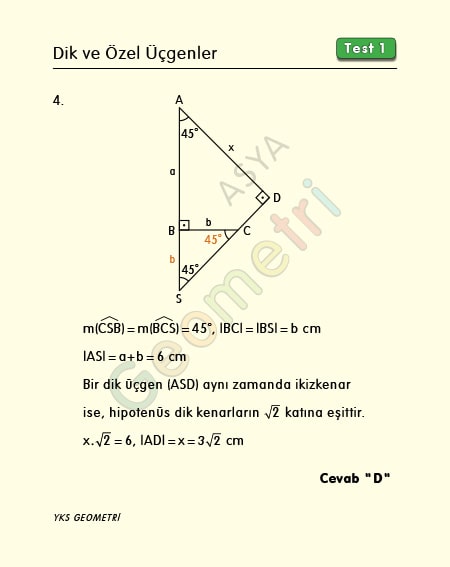
Problem 4 :
If [AB] perpendicular [BC], [CD] perpendicular [AD], m (BAD) = 45 °, | AB | + | BC | = 6 cm; what is the length of AD?
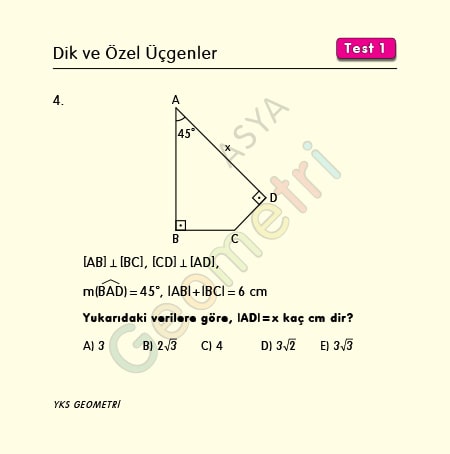
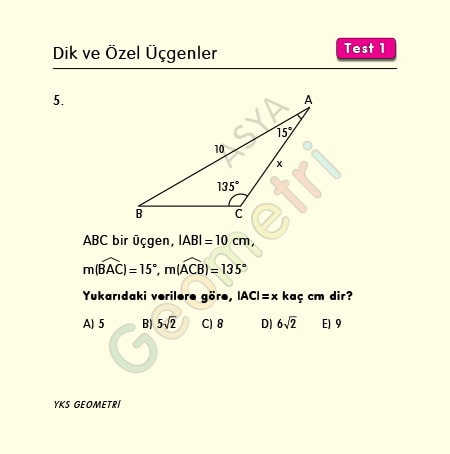
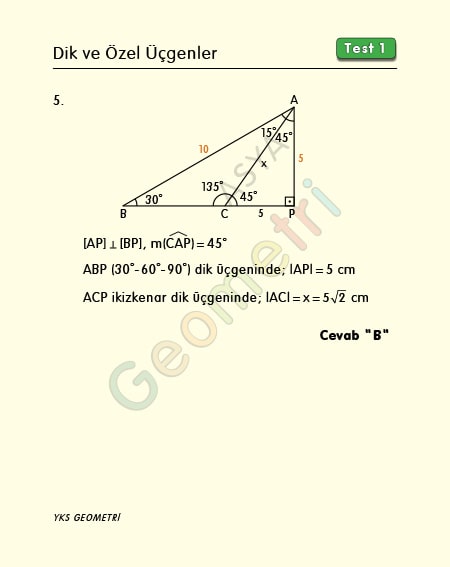
Problem 5 :
ABC is a triangle, if | AB | = 10 cm, m (BAC) = 15 °, m (ACB) = 135 °; what is the length of AC?
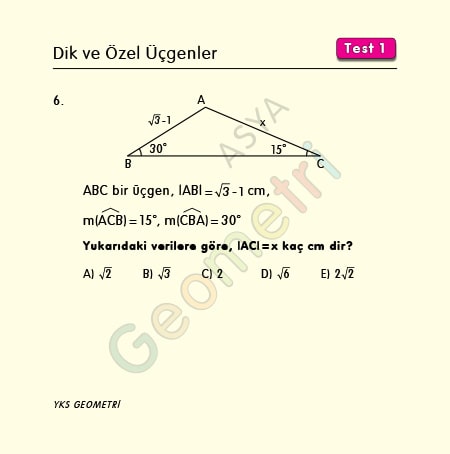
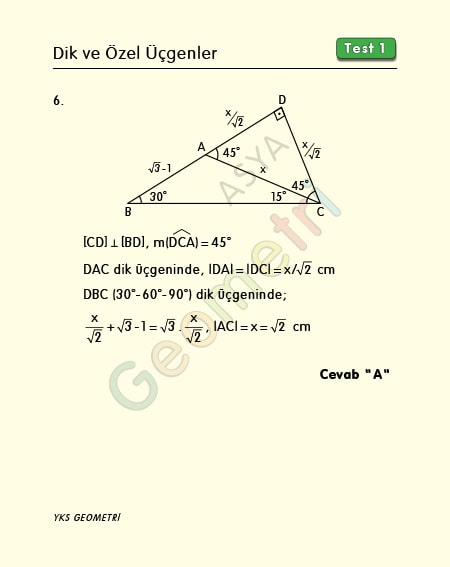
Problem 6 :
If ABC is a triangle, | AB | = √3 -1 cm, m (ACB) = 15 °, m (CBA) = 30 °; what is the length of AC?
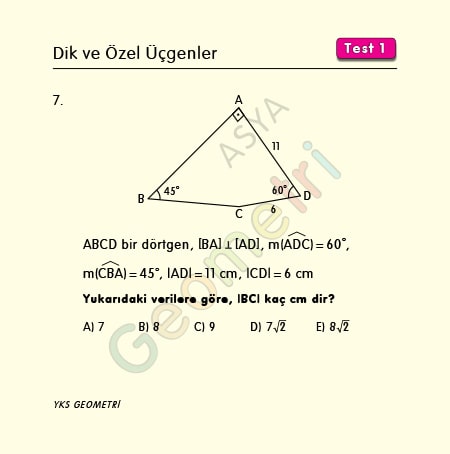
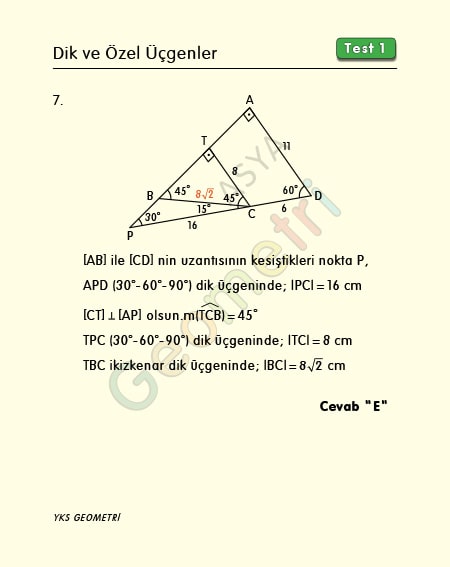
Problem 7 :
ABCD is a quadrilateral, if [BA] perpendicular [AD], m (ADC) = 60 °, m (CBA) = 45 °, | AD | = 11 cm, | CD | = 6 cm; what is the length of BC?
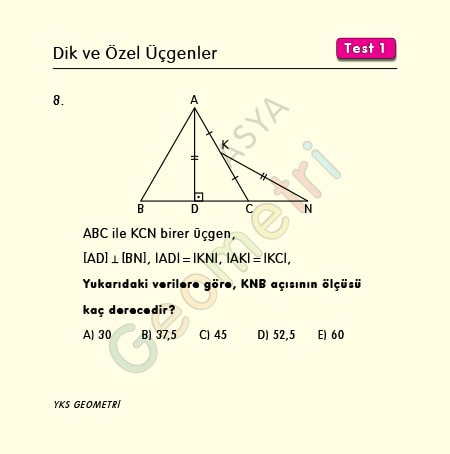
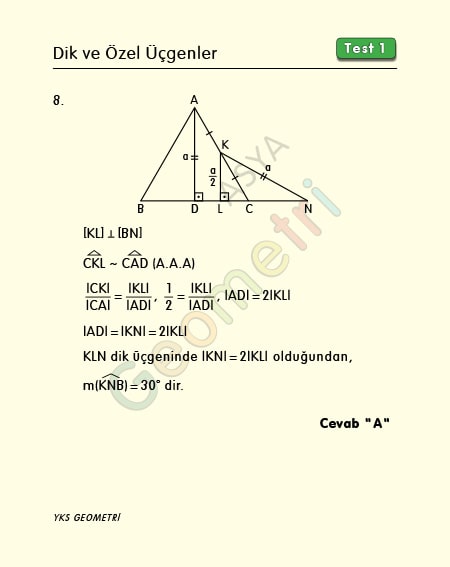
Problem 8 :
ABC and KCN are each triangle, [AD] perpendicular [BN], | AD | = | KN |, | AK | = | KC | if; What is the measure of the KNB angle?
Special Right Triangle Test-1 Solutions
Solution of Problem 1 :
In an ABC isosceles triangle (| AC | = | BC |), if a point of the base [BC] is D; | AD | ² = | AB | ²- | BD |. | DC | (x² = b-m.n).
7² = 9²- | BD |. | DC | If written, | BD |. | DC | = 32 cm².

Solution of Problem 2.1 :
From the Pythagorean relation in ABC triangle | BC | = k.√5. If we say | BD | = x; | DC | = k√5-x. In triangle ABC k² = x.k√5, x = k / √5 from the Euclidean relation. If k / root5 is written instead of x, since k = 2 √5, then | BC | = 10 cm.
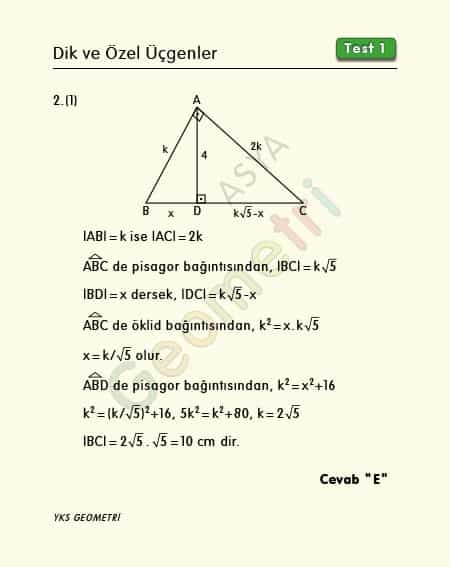
Solution of Problem 2.2 :
The height of the hypotenuse in a right triangle is found by dividing the product of perpendicular sides by the hypotenuse. This is called the area relation. It is covered with the subject of the Euclidean theorem. For the proof of this formula and to prove other formulas, see the geometry proof section.
Solution of Problem 3 :
Solution 3: In a right triangle, the height of the hypotenuse squared is equal to the product of the lengths it separates from the corners. This is called the Euclidean theorem.

Solution of Problem 4 :
If the right triangle is also isosceles, then the hypotenuse is equal to the root2 times the perpendicular sides.
Solution of Problem 5 :
Let’s straighten the extension BC from corner A. Write instead of angles and call edge 5 opposite 30 °. Since the hypotenuse is equal to the √2 of the right sides in an isosceles right triangle, we write 5√2 for the length AC.
Solution of Problem 6 :
There are many solutions to these questions. We can solve them practically by creating a 30 60 90 triangle or a 45 45 90 triangle.
Solution of Problem 7 :
In 30 60 90 triangle, the side opposite 30 ° is half the length of the hypotenuse, and in an isosceles right triangle the hypotenuse is equal to the root of the right sides.
Solution of Problem 8 :
In a right triangle, if one of the right sides is equal to half the length of the hypotenuse, this triangle is 30 60 90 and the opposite corner is 30 °.

Special Right Triangles Test-1 PDF
Course Geometry offers Geometry textbook in pdf format that can be downloaded free of charge. Students can view the special right triangles test-1 pdf, which is important for university entrance exam, which aims to improve students’ problem solving skills.