Special Right Triangles Test-4

Special Right Triangles Test-4 …

Special Right Triangles Test-4 Problems

Problem 1 :

ABC is a triangle, [CK] perpendicular [AB], [EP] perpendicular [AB], [ED] perpendicular [AD], | AB | = | AC |, | PE | + | KC | = 2 | If BC |, | KB | = root17 cm, | ED | = 2 cm; | BC | how many cm?

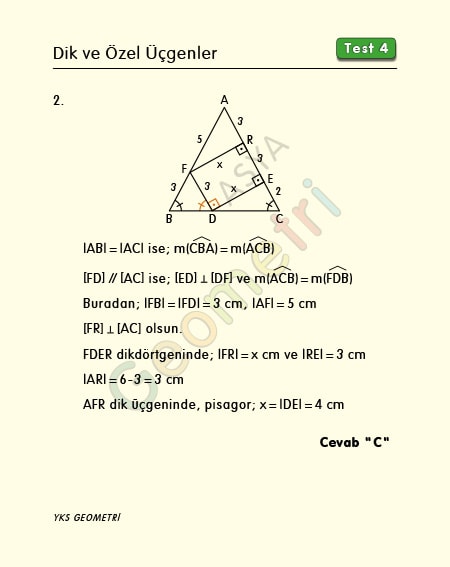
Problem 2 :

Question 2-) In triangle ABC | AB | = | AC |, [FD] parallel [AC], [DE] perpendicular [AC], | AE | = 6 cm, | EC | = 2 cm, | FB | = 3 cm if; | DE | = how many cm is x?

Problem 3 :

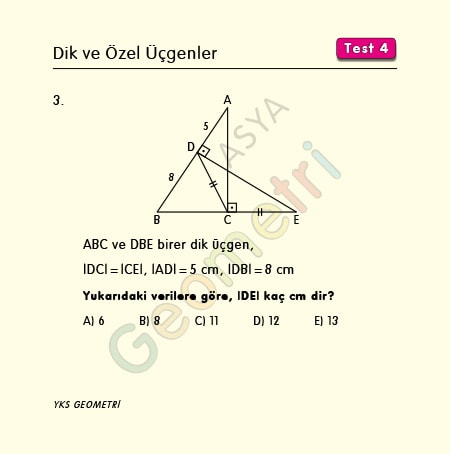
If ABC and DBE are right triangles, | DC | = | CE |, | AD | = 5 cm, | DB | = 8 cm; | DE | how many cm?

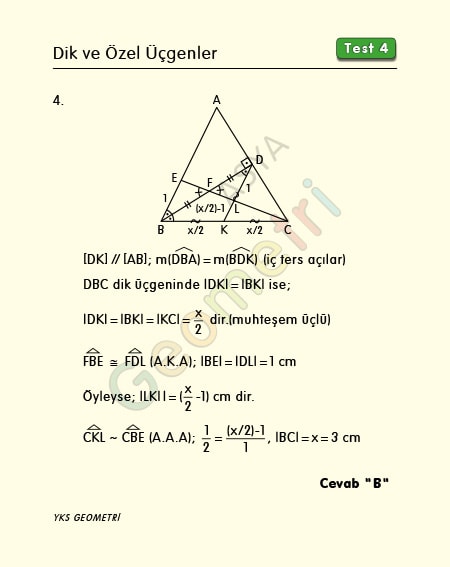
Problem 4 :

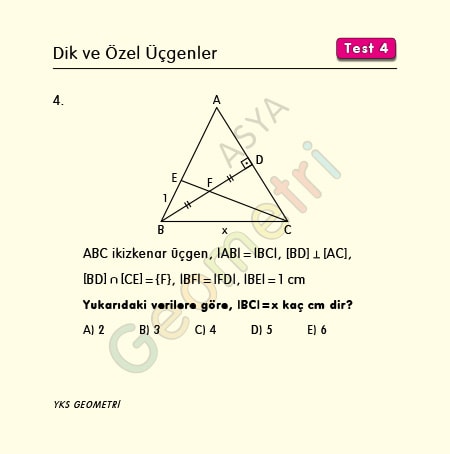
ABC isosceles triangle, | AB | = | BC |, [BD] perpendicular [AC], [BD] and the cut-off point of [CE] F, | BF | = | FD |, | BE | = 1 cm , | BC | = how many cm is x?

Problem 5 :

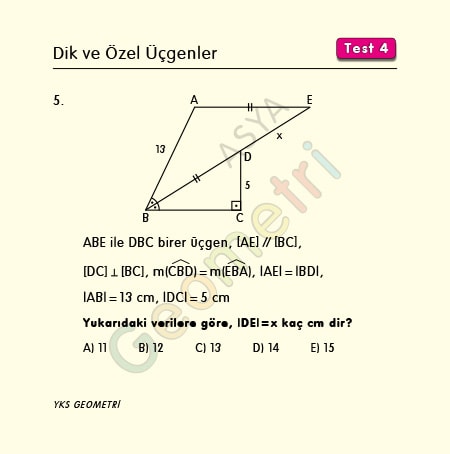
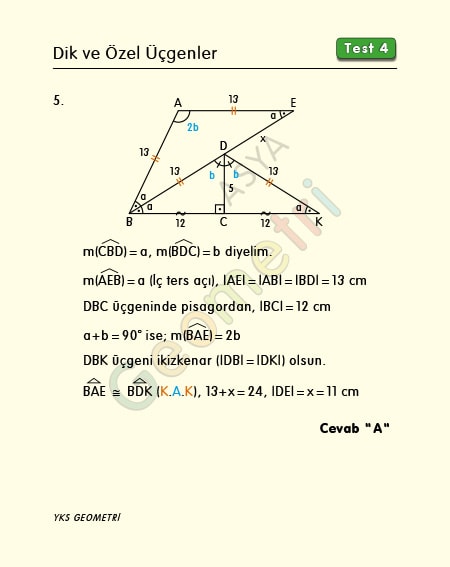
ABE and DBC are each triangle, [AE] parallel [BC], [DC] perpendicular [BC], m (CBD) = m (EBA), | AE | = | BD |, | AB | = 13 cm If | DC | = 5 cm; | DE | = how many cm is x?

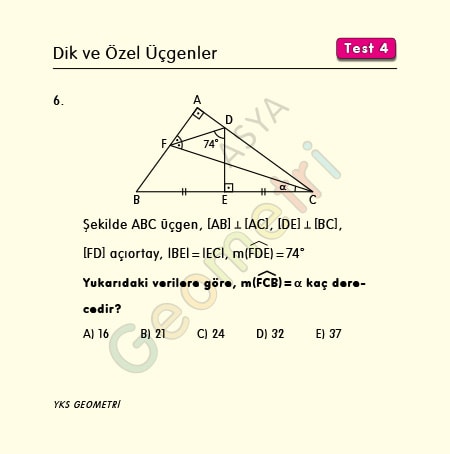
Problem 6 :

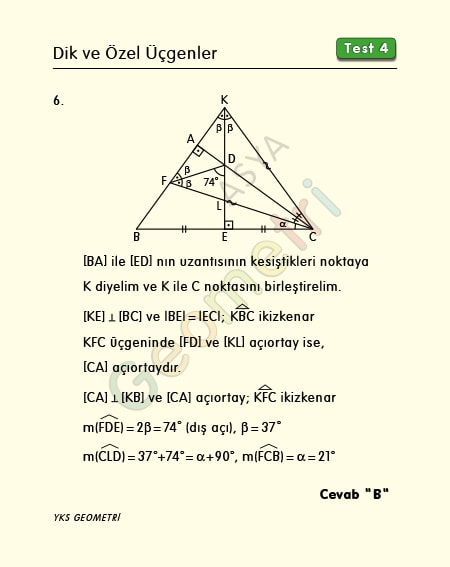
If ABC is triangle in the figure, [AB] perpendicular [AC], [DE] perpendicular [BC], [FD] bisector, | BE | = | EC |, if m (FDE) = 74 °; How many degrees is m (FCB) = α?

Problem 7 :

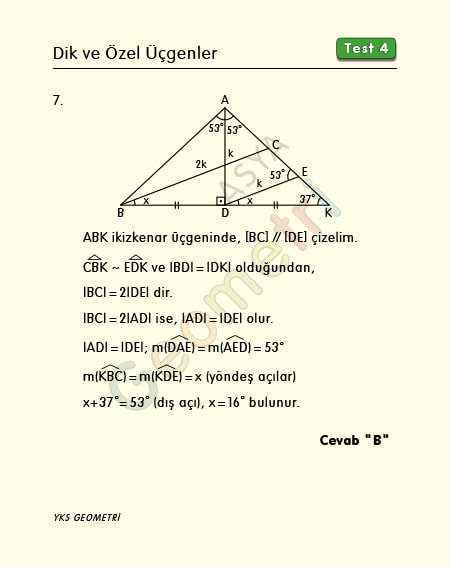
If ABC triangle, [AD] perpendicular [BD], | BC | = 2 | AD |, m (BAD) = m (DAC) = 53 °; How many degrees is m (DBC) = x?

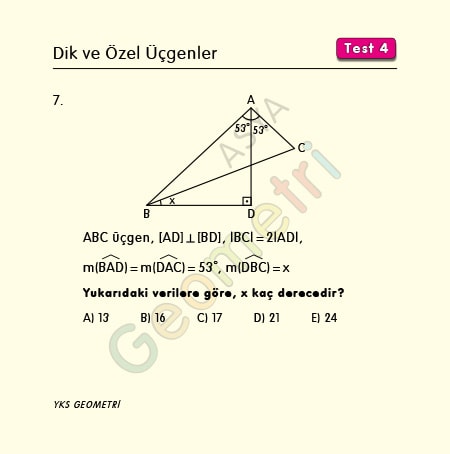
Problem 8 :

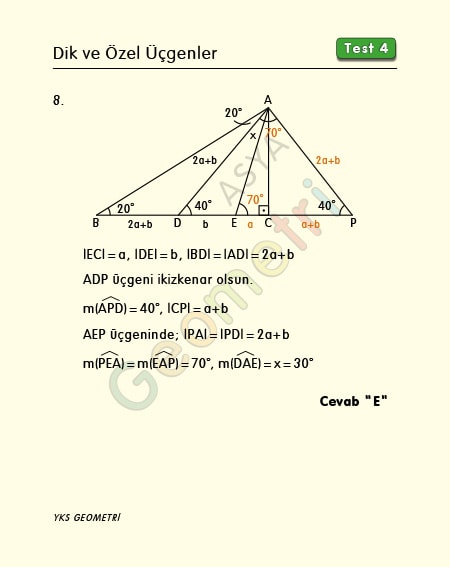
ABC right triangle, if | BE | = 2 | CD |, m (CBA) = 20 °, m (CDA) = 40 °; How many degrees is m (DAE) = x?

Special Right Triangle Test-4 Solutions

Solution of Problem 1 :

If we say | BC | = x, we have | PE | + | KC | = 2x. In the isosceles triangle ABC | PE | = | KC | + | ED | | KC | +2+ | KC | = 2x, from here | KC | = x-1. If the Pythagorean relation is written in the KBC triangle, | BC | = x = 9 cm.

Solution of Problem 2 :

In the isosceles triangle ABC, [FD] is parallel to [AC], and [DF] is perpendicular to the corresponding angles | FD | = 3 cm and [ED], since FDER is rectangular | FR | = x cm, | RE | = 3 cm, | AF | = 8-3 = 5 cm, | AR | = 6-3 = 3 cm, in AFR right triangle there is x = 4 cm from the pythagoras.

Solution of Problem 3 :

In the DBC right triangle | DC | = | CE | is | DC | = | BC | = | CE | (the magnificent triad). | BC | = | CE | And since it is perpendicular to [AC] and [BE], if we connect points A with E, the triangle ABE becomes isosceles. | AC | = 13 cm. Since the triangle of AD will have a 5-12-13 right triangle, | DE | = 12 cm.

Solution of Problem 4 :

In DBC triangle | DK | = | BK | is | DK | = | BK | = | KC | (magnificent triple). Since | DL | = 1 cm from the same triangles, | DK | = (x / 2) -1. From the similarity of the two triangles, x = 3 cm.

Solution of Problem 5 :

Since the angles between the two sides of the isosceles triangle DBK and the triangle ABE are equal, these triangles are equal. Since DBC will be 5-12-13 right triangle, | BC | = 12 cm. | BK | = | BE | = 24 cm. From here | DE | = x = 24-13 = 11 cm is calculated.

Solution of Problem 6 :

Let’s connect the point K where the extension of [BA] and [ED] intersects to point C. KBC is an isosceles triangle since the height is also median. If a triangle has two inner bisectors, the third is the bisector. According to this, in KFC triangle [CA] is bisector. Since [CA] is bisector and height, KFC triangle is isosceles. If we call the base angles 2β, it is = 37 ° from the external angle. Since m (CLD) = 37 ° + 74 ° = α + 90 °, m (FCB) = α = 21 °.

Solution of Problem 7 :

The point K where [AC] and the extension of [BD] intersect makes the triangle ABK isosceles. If we draw parallel to [AK] from point D, | BD | = | DK | Since the triangles have a similarity ratio of 2, | BC | = 2 | DE | dir. | BC | = 2 | AD | was. Accordingly | AD | = | DE | Since it will be, m (AED) = 53 ° and m (KDE) = x from corresponding angles. x + 37 ° = 53 °, x = 16 ° are calculated.

Solution of Problem 8 :

Outside angle m (BAD) = 20 °. Since m (CBA) = m (BAD) = 20 ° | BD | = | AD | Dir. | EC | = a, | DE | = b, then | BD | = 2a + b. | BD | = | AD | = 2a + b. Let’s take a point P such that the triangle ADP is isosceles. m (APD) = 40 °, | CP | = a + b. Since | AP | = | EP | = 2a + b, in AEP triangle m (PEA) = m (EAP) = 70 °. x + 40 ° = 70 °, x = 30 °.

Special Right Triangles Test-4 PDF

Course Geometry offers Geometry textbook in pdf format that can be downloaded free of charge. Students can view the special right triangles test-4 pdf, which is important for university entrance exam, which aims to improve students’ problem solving skills.